
分析 根据不等式组的解集即可得出关于a、b而愿意方程组,解方程组即可得出a、b值,将其代入方程ax+b=0中,解出方程即可得出结论.
解答 解:∵不等式组$\left\{\begin{array}{l}{x+1<2a}\\{x-b>1}\end{array}\right.$的解集是2<x<3,
∴$\left\{\begin{array}{l}{2a-1=3}\\{b+1=2}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=2}\\{b=1}\end{array}\right.$,
∴方程ax+b=0为2x+1=0,
解得:x=-$\frac{1}{2}$.
故答案为:-$\frac{1}{2}$.
点评 本题考查了解一元一次不等式以及一元一次方程的解,解题的关键是求出a、b值.本题属于基础题,难度不大,解集该题型题目时,根据不等式组的解集求出未知数的值是关键.


科目:初中数学 来源: 题型:解答题
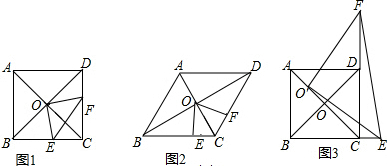
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
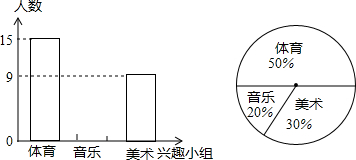
| A. | 八年级(1)班参加这三个课外兴趣小组的学生总人数为30人 | |
| B. | 在扇形统计图中,八年级(1)班参加音乐兴趣小组的学生人数所占的圆心角度数为82° | |
| C. | 八年级(1)班参加音乐兴趣小组的学生人数为6人 | |
| D. | 若该校八年级参加这三个兴趣小组的学生共有200人,那么估计全年级参加美术兴趣小组的学生约有60人 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
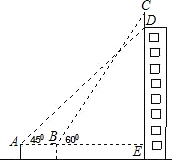 如图某幢大楼顶部有一广告牌CD,甲、乙两人分别在相距8米的A、B两处测得D点和C点的仰角分别为45°和60°,且A、B、E三点在一直线(∠AEC=90°)上,若BE=15米,求这块广告牌的CD.(取 $\sqrt{3}$=1.73,计算结果保留整数)
如图某幢大楼顶部有一广告牌CD,甲、乙两人分别在相距8米的A、B两处测得D点和C点的仰角分别为45°和60°,且A、B、E三点在一直线(∠AEC=90°)上,若BE=15米,求这块广告牌的CD.(取 $\sqrt{3}$=1.73,计算结果保留整数)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1200}{x}$-$\frac{1200}{(1+20%)x}$=2 | B. | $\frac{1200}{(1-20%)x}$-$\frac{1200}{x}$=2 | ||
| C. | $\frac{1200}{(1+20%)x}$-$\frac{1200}{x}$=2 | D. | $\frac{1200}{x}$-$\frac{1200}{(1-20%)x}$=2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
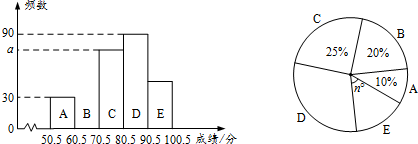
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com