
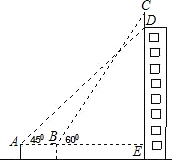
 如图某幢大楼顶部有一广告牌CD,甲、乙两人分别在相距8米的A、B两处测得D点和C点的仰角分别为45°和60°,且A、B、E三点在一直线(∠AEC=90°)上,若BE=15米,求这块广告牌的CD.(取 $\sqrt{3}$=1.73,计算结果保留整数)
如图某幢大楼顶部有一广告牌CD,甲、乙两人分别在相距8米的A、B两处测得D点和C点的仰角分别为45°和60°,且A、B、E三点在一直线(∠AEC=90°)上,若BE=15米,求这块广告牌的CD.(取 $\sqrt{3}$=1.73,计算结果保留整数) 科目:初中数学 来源: 题型:填空题
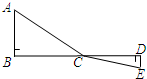 阅读材料:如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.设CD=x,若AB=4,DE=2,BD=8,则可用含x的代数式表示AC+CE的长为$\sqrt{16+(8-x)^{2}}$+$\sqrt{4+{x}^{2}}$.然后利用几何知识可知:当A、C、E在一条直线上时,x=$\frac{8}{3}$时,AC+CE的最小值为10.根据以上阅读材料,可构图求出代数式$\sqrt{25+(12-x)^{2}}$+$\sqrt{9+{x}^{2}}$的最小值为4$\sqrt{13}$.
阅读材料:如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.设CD=x,若AB=4,DE=2,BD=8,则可用含x的代数式表示AC+CE的长为$\sqrt{16+(8-x)^{2}}$+$\sqrt{4+{x}^{2}}$.然后利用几何知识可知:当A、C、E在一条直线上时,x=$\frac{8}{3}$时,AC+CE的最小值为10.根据以上阅读材料,可构图求出代数式$\sqrt{25+(12-x)^{2}}$+$\sqrt{9+{x}^{2}}$的最小值为4$\sqrt{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某生在旗杆EF与实验楼CD之间的A处,测得∠EAF=60°,然后向左移动12米到B处,测得∠EBF=30°,∠CBD=45°,sin∠CAD=$\frac{3}{5}$.
如图,某生在旗杆EF与实验楼CD之间的A处,测得∠EAF=60°,然后向左移动12米到B处,测得∠EBF=30°,∠CBD=45°,sin∠CAD=$\frac{3}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com