
分析 (1)将点A的坐标代入直线解析式求出a的值,继而将点A的坐标代入抛物线解析式可得出b的值,继而得出抛物线解析式;
(2)根据点B的横坐标为m,表示出点B的坐标是(m,$\frac{1}{2}$m2-m),点E的坐标为(m,2m),根据A,O点坐标得出C点坐标,进而得出m的值即可得出答案.
解答 解:(1)∵点A(a,12)在直线y=2x上,
∴12=2a,
解得:a=6,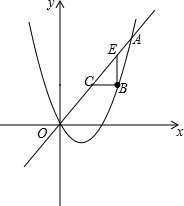
又∵点A是抛物线y=$\frac{1}{2}$x2+bx上的一点,
将点A(6,12)代入y=$\frac{1}{2}$x2+bx,可得b=-1,
∴抛物线解析式为y=$\frac{1}{2}$x2-x.
(2)如图所示:∵点B的横坐标为m,
∴点B的坐标是(m,$\frac{1}{2}$m2-m),点E的坐标为(m,2m),
∴BE=2m-($\frac{1}{2}$m2-m)=-$\frac{1}{2}$(m-3)2+$\frac{9}{2}$,
∵C为AO的中点,
∴C(3,6),
∴$\frac{1}{2}$m2-m=6,
解得:m1=1+$\sqrt{13}$,m2=1-$\sqrt{13}$(不合题意舍去),
∴BE=-$\frac{1}{2}$(m-3)2+$\frac{9}{2}$=-$\frac{1}{2}$(1+$\sqrt{13}$-3)2+$\frac{9}{2}$=2$\sqrt{13}$-4.
点评 此题考查了二次函数的性质、配方法、待定系数法求二次函数解析式的知识,表示出C、E、B点坐标是解题关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
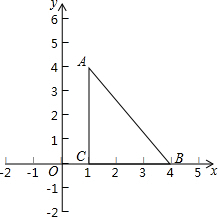 如图,在平面直角坐标系中,点A(1,4),点B(4,0),点C(1,0).
如图,在平面直角坐标系中,点A(1,4),点B(4,0),点C(1,0).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 解一元一次方程的过程就是通过变形,把一元一次方程转化为x=a的形式.下面是解方程$\frac{2x-0.3}{0.5}-\frac{x+0.4}{0.3}=1$的主要过程,请在如图的矩形框中选择与方程变形对应的依据,并将它前面的序号填入相应的括号中.
解一元一次方程的过程就是通过变形,把一元一次方程转化为x=a的形式.下面是解方程$\frac{2x-0.3}{0.5}-\frac{x+0.4}{0.3}=1$的主要过程,请在如图的矩形框中选择与方程变形对应的依据,并将它前面的序号填入相应的括号中.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某产品每件成本28元,在试销阶段产品的日销售量y(件)与每件产品的日销售价x(元)之间的关系如图中的折线所示.为维持市场物价平衡,最高售价不得高出83元.
某产品每件成本28元,在试销阶段产品的日销售量y(件)与每件产品的日销售价x(元)之间的关系如图中的折线所示.为维持市场物价平衡,最高售价不得高出83元.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com