
【题目】如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE. 
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.
【答案】
(1)证明:∵△BAD是由△BEC在平面内绕点B旋转60°而得,
∴DB=CB,∠ABD=∠EBC,∠ABE=60°,
∵AB⊥EC,
∴∠ABC=90°,
∴∠DBE=∠CBE=30°,
在△BDE和△BCE中,
∵ 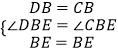 ,
,
∴△BDE≌△BCE
(2)四边形ABED为菱形;
由(1)得△BDE≌△BCE,
∵△BAD是由△BEC旋转而得,
∴△BAD≌△BEC,
∴BA=BE,AD=EC=ED,
又∵BE=CE,
∴四边形ABED为菱形
【解析】(1)根据旋转的性质可得DB=CB,∠ABD=∠EBC,∠ABE=60°,然后根据垂直可得出∠DBE=∠CBE=30°,继而可根据SAS证明△BDE≌△BCE;(2)根据(1)以及旋转的性质可得,△BDE≌△BCE≌△BDA,继而得出四条棱相等,证得四边形ABED为菱形.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形 ABCD 的对角线 AC 与 BD 相交于点 O,CE∥BD,DE∥AC.
(1)求证:四边形 OCED 为菱形
(2)若AD=7,AB=4,求四边形 OCED的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,∠C=90°,点D是AB的中点,点E,F分别在BC,AC上,且AF=CE.
(1)填空:∠A的度数是 .
(2)探究DE与DF的关系,并给出证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P以1cm/秒的速度沿折线BE﹣ED﹣DC运动到点C时停止,点Q以2cm/秒的速度沿BC运动到点C时停止.设P、Q同时出发t秒时,△BPQ的面积为ycm2 . 已知y与t的函数关系图像如图(2)(其中曲线OG为抛物线的一部分,其余各部分均为线段).
(1)试根据图(2)求0<t≤5时,△BPQ的面积y关于t的函数解析式;
(2)求出线段BC、BE、ED的长度;
(3)当t为多少秒时,以B、P、Q为顶点的三角形和△ABE相似;
(4)如图(3)过E作EF⊥BC于F,△BEF绕点B按顺时针方向旋转一定角度,如果△BEF中E、F的对应点H、I恰好和射线BE、CD的交点G在一条直线,求此时C、I两点之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个水池,用两根水管注水,如果单开甲管,5小时注满水池,如果单开乙管,10小时注满水池.
(1)如果甲先注水2小时,然后由甲、乙共同注水,那么还需要多少时间才能把水池注满?
(2)假设在水池下面安装了排水管丙管,单开丙管6小时可以把一满池水放完,如果三管同时开放,多少小时才能把一空池注满水?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分校为了调查初三年级学生每周的课外活动时间,随机抽查了50名初三学生,对其平均毎周参加课外活动的时间进行了调查.由调查结果绘制了频数分布直方图,根据图中信息回答下列问题: 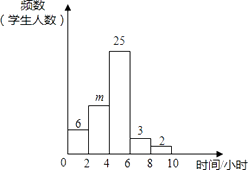
(1)求m的值;
(2)计算50名学生的课外活动时间的平均数(每组时间用其组中值表示),对初三年级全体学生平均每周的课外活动吋问做个推断;
(3)从参加课外活动时间在6~10小时的5名学生中随机选取2人,请你用列表法,求其中至少有1人课外活动时间在8~10小时的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为喜迎祖国![]() 周年华诞,某巡警骑摩托车在天安门前的东西大街上巡逻,某天他从天安门出发,晚上留在
周年华诞,某巡警骑摩托车在天安门前的东西大街上巡逻,某天他从天安门出发,晚上留在![]() 处,规定向东方向为正,当天他的行驶记录如下(单位:
处,规定向东方向为正,当天他的行驶记录如下(单位:![]() ):
):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 处在天安门的何方?相距多少千米?
处在天安门的何方?相距多少千米?
![]() 若摩托车耗油
若摩托车耗油![]() ,问这一天摩托车共耗油多少升?
,问这一天摩托车共耗油多少升?
![]() 在这一天中,该巡警与天安门相距最远时是多少千米?
在这一天中,该巡警与天安门相距最远时是多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,BC=12,CD=9,将△ABE沿BE折叠,使点A恰好落在对角线BD上的F处,则DE的长是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在密码学中,直接可以看到的内容为明码,对明码进行某种处理后得到的内容为密码,有一种密码,将英文26个字母a,b,c,…,z(不论大写)依次对应1,2,3,…,26,这26个自然数,当明码字母对应的序号x为奇数时,密码字母对应的序号是![]() ;当明码字母对应的序号x为偶数时,密码存对应的序号是
;当明码字母对应的序号x为偶数时,密码存对应的序号是![]() .按上述规定,将明码"hope”译成密码是( )
.按上述规定,将明码"hope”译成密码是( )

A. gawp B. rivd C. gihe D. hope
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com