
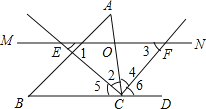
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=8,CF=6,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?
并说明理由.

【答案】(1)证明见解析;(2)5;(3)当点O在边AC上运动到AC中点时,四边形AECF是矩形.证明见解析.
【解析】试题分析:(1)根据平行线的性质以及角平分线的性质得出∠1=∠2,∠3=∠4,进而得出答案;(2)根据已知得出∠2+∠4=∠5+∠6=90°,进而利用勾股定理求出EF的长,即可得出CO的长;(3)根据平行四边形的判定以及矩形的判定得出即可.
试题解析:(1)证明:∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
∴∠2=∠5,∠4=∠6,
∵MN∥BC,
∴∠1=∠5,∠3=∠6,
∴∠1=∠2,∠3=∠4,
∴EO=CO,FO=CO,
∴OE=OF;
(2)∵∠2=∠5,∠4=∠6,
∴∠2+∠4=∠5+∠6=90°,
∵CE=8,CF=6,
∴EF=![]() =10,
=10,
∴OC=![]() EF=5;
EF=5;
(3)当点O在边AC上运动到AC中点时,四边形AECF是矩形.
证明:当O为AC的中点时,AO=CO,
∵EO=FO,
∴四边形AECF是平行四边形,
∵∠ECF=90°,
∴平行四边形AECF是矩形.


科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠BAD=2∠B,E,F分别为BC,CD的中点,连接AE、AC、AF,则图中与△ABE全等的三角形(△ABE除外)有

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】方程2x2+4x-3=0的二次项系数、一次项系数、常数项分别是( )
A. 2,-3,-4 B. 2,-4,-3
C. 2,-4,3 D. 2,4,-3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市四月份连续五天的日最高气温分别为23、20、20、21、26(单位:℃),这组数据的中位数和众数分别是( )
A.21℃,20℃
B.21℃,26℃
C.22℃,20℃
D.22℃,26℃
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系内,把点P(-5,-2)先向左平移2个单位长度,再向上平移4个单位长度后得到的点的坐标是
A. (-3,2)B. (-7,-6)C. (-7,2)D. (-3,-6)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com