
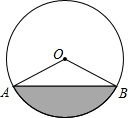
 下图是输水管的切面,阴影部分是有水部分,其中水面AB宽16cm,水最深4cm.
下图是输水管的切面,阴影部分是有水部分,其中水面AB宽16cm,水最深4cm.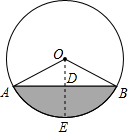 解:(1)设圆形切面的半径,过点O作OD⊥AB于点D,交⊙O于点E,
解:(1)设圆形切面的半径,过点O作OD⊥AB于点D,交⊙O于点E,| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 3 |
| 120×π×102 |
| 360 |
| 1 |
| 2 |
| 3 |
100π-75
| ||
| 3 |


科目:初中数学 来源: 题型:
 如图所示,在宽为25m,长为36m的矩形耕地上,修筑同样宽的三条道路,(互相垂直),把耕地分成大小不等的六块试验田,要使试验田的面积为590m2,道路应为多宽?若设道路的宽为x米,根据题意可列方程
如图所示,在宽为25m,长为36m的矩形耕地上,修筑同样宽的三条道路,(互相垂直),把耕地分成大小不等的六块试验田,要使试验田的面积为590m2,道路应为多宽?若设道路的宽为x米,根据题意可列方程查看答案和解析>>
科目:初中数学 来源: 题型:
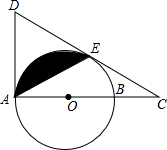 如图,AB是⊙的直径,AD切⊙O于A,延长AB到C,过C作⊙O的切线CE,切点为E,CE的延长线交AD于D,连接AE,且AE=CE.
如图,AB是⊙的直径,AD切⊙O于A,延长AB到C,过C作⊙O的切线CE,切点为E,CE的延长线交AD于D,连接AE,且AE=CE.查看答案和解析>>
科目:初中数学 来源: 题型:
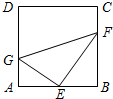 如图,在正方形ABCD中,E为AB边的中点,G,F分别为AD,BC边上的点,若AG=1,BF=2,∠GEF=90°,则GF的长为( )
如图,在正方形ABCD中,E为AB边的中点,G,F分别为AD,BC边上的点,若AG=1,BF=2,∠GEF=90°,则GF的长为( )| A、3 | B、4 | C、5 | D、6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com