
分析 (1)根据代入消元法可以解答本题;
(2)根据加减消元法可以解答本题.
解答 解:(1)$\left\{\begin{array}{l}{y=x-3}&{①}\\{y-2x=5}&{②}\end{array}\right.$,
把①代入②,得
x-3-2x=5,
解得,x=-8,
把x=-8代入①,得
y=-11,
∴原方程组的解是$\left\{\begin{array}{l}x=-8\\ y=-11\end{array}\right.$;
(2)$\left\{\begin{array}{l}{4x+y=5}&{①}\\{3x-2y=1}&{②}\end{array}\right.$,
由①×2,得
8x+2y=10 ③
②+③,得
11x=11
解得,x=1
把x=1代入①,得
y=1
∴原方程组的解是$\left\{\begin{array}{l}x=1\\ y=1\end{array}\right.$.
点评 本题考查解二元一次方程组,解答本题的关键是明确解二元一次方程组的方法.


科目:初中数学 来源: 题型:解答题
 城市规划期间,欲拆除一电线杆AB,如图,已知大坝背水坡ED的坡角∠EDG=60°,背水坡ED的垂直高度EH为6米,在坝顶E处有一高为1米的测角仪EF,测得杆顶A的仰角为20°,杆底B的俯角为20°,C、D之间是2米宽的人行道,在拆除电线杆AB时,为确保行人安全,是否需要将此人行道封闭?请说明理由(在地面上,以点B为圆心,以AB为半径的圆形区域为危险区域).(tan20°≈0.4,tan70°≈2.7,$\sqrt{3}$≈1.7)
城市规划期间,欲拆除一电线杆AB,如图,已知大坝背水坡ED的坡角∠EDG=60°,背水坡ED的垂直高度EH为6米,在坝顶E处有一高为1米的测角仪EF,测得杆顶A的仰角为20°,杆底B的俯角为20°,C、D之间是2米宽的人行道,在拆除电线杆AB时,为确保行人安全,是否需要将此人行道封闭?请说明理由(在地面上,以点B为圆心,以AB为半径的圆形区域为危险区域).(tan20°≈0.4,tan70°≈2.7,$\sqrt{3}$≈1.7)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知,如图,线段AB,利用无刻度的直尺和圆规,作一个满足条件的△ABC:①△ABC为直角三角形;②tan∠A=$\frac{1}{3}$.(注:不要求写作法,但保留作图痕迹)
已知,如图,线段AB,利用无刻度的直尺和圆规,作一个满足条件的△ABC:①△ABC为直角三角形;②tan∠A=$\frac{1}{3}$.(注:不要求写作法,但保留作图痕迹)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知△ABC中,∠ACB=90°,且AC=BC.过点C作一条射线CE⊥AE于点E,再过点B作BD⊥CE于点D.试证明AE=BD+DE.
如图,已知△ABC中,∠ACB=90°,且AC=BC.过点C作一条射线CE⊥AE于点E,再过点B作BD⊥CE于点D.试证明AE=BD+DE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图:在△ABC中,CE、CF分别平分∠ACB与它的邻补角∠ACD,AE⊥CE于E,AF⊥CF于F,直线EF分别交AB、AC于M、N.
如图:在△ABC中,CE、CF分别平分∠ACB与它的邻补角∠ACD,AE⊥CE于E,AF⊥CF于F,直线EF分别交AB、AC于M、N.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
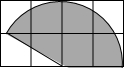 如图所示的格点纸中每个小正方形的边长均为1,以小正方形的顶点为圆心,2为半径做了一个扇形,用该扇形围成一个圆锥的侧面,针对此做法,小明和小亮通过计算得出以下结论:小明说此圆锥的侧面积为$\frac{5}{3}$π;小亮说此圆锥的弧长为$\frac{5}{3}$π,则下列结论正确的是( )
如图所示的格点纸中每个小正方形的边长均为1,以小正方形的顶点为圆心,2为半径做了一个扇形,用该扇形围成一个圆锥的侧面,针对此做法,小明和小亮通过计算得出以下结论:小明说此圆锥的侧面积为$\frac{5}{3}$π;小亮说此圆锥的弧长为$\frac{5}{3}$π,则下列结论正确的是( )| A. | 只有小明对 | B. | 只有小亮对 | C. | 两人都对 | D. | 两人都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的,若AC=4,BC=6,将四个直角三角形中边长为4的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是( )
如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的,若AC=4,BC=6,将四个直角三角形中边长为4的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是( )| A. | 56 | B. | 24 | C. | 64 | D. | 32 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com