
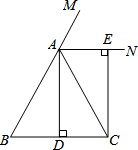
 已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,猜想四边形ADCE的形状,并给予证明.
已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,猜想四边形ADCE的形状,并给予证明. 分析 根据AN是△ABC外角∠CAM的平分线,推得∠MAE=$\frac{1}{2}$(∠B+∠ACB),再由∠B=∠ACB,得∠MAE=∠B,则AN∥BC,根据CE⊥AN,得出四边形ADCE为矩形.
解答 证明:∵AN是△ABC外角∠CAM的平分线,
∴∠MAE=$\frac{1}{2}$∠MAC,
∵∠MAC=∠B+∠ACB,
∵AB=AC,
∴∠B=∠ACB,
∴∠MAE=∠B,
∴AN∥BC,
∵AB=AC,点D为BC中点,
∴AD⊥BC,
∵CE⊥AN,
∴AD∥CE,
∴四边形ADCE为平行四边形(有两组对边分别平行的四边形是平行四边形),
∵CE⊥AN,
∴∠AEC=90°,
∴四边形ADCE为矩形(有一个角是直角的平行四边形是矩形).
点评 此题考查了矩形的判定与性质、三线合一以及三角形中位线的性质.此题难度适中,注意掌握数形结合思想的应用.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:选择题
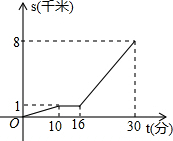 小亮从家O,步行到公交站台B,等公交车去学校C,图中的折线表示小亮的行程s(千米)与所花时间t(分)之间的函数关系.下列说法错误的是( )
小亮从家O,步行到公交站台B,等公交车去学校C,图中的折线表示小亮的行程s(千米)与所花时间t(分)之间的函数关系.下列说法错误的是( )| A. | 他家到公交车站台为1千米 | B. | 他等公交车的时间为6分钟 | ||
| C. | 他步行的速度100米/分钟 | D. | 公交车的速度是350米/分钟 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}x=2y+1\\ y=3-z\end{array}\right.$ | B. | $\left\{\begin{array}{l}xy=12\\ x+y=7\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}x=3\\ y=4\end{array}\right.$ | D. | $\left\{\begin{array}{l}\frac{1}{x}+\frac{1}{y}=2\\ 3x-2y=4\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1,2 | B. | 1,3 | C. | 5,1 | D. | 2,4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
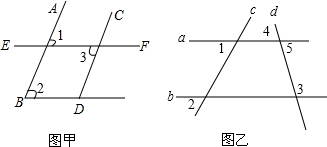 (1)如图甲:∠1=∠2=∠3,完成说理过程并注明理由:
(1)如图甲:∠1=∠2=∠3,完成说理过程并注明理由:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com