
【题目】某商场经营某种品牌的童装,购进时的单价是![]() 元.根据市场调查,在一段时间内,销售单价是
元.根据市场调查,在一段时间内,销售单价是![]() 元时,销售量是
元时,销售量是![]() 件.而销售单价每降低
件.而销售单价每降低![]() 元,就可多售出
元,就可多售出![]() 件.
件.
![]() 求出销售该品牌童装获得的利润
求出销售该品牌童装获得的利润![]() 元与销售单价
元与销售单价![]() 元之间的函数关系式;
元之间的函数关系式;
![]() 若童装厂规定该品牌童装销售单价不低于
若童装厂规定该品牌童装销售单价不低于![]() 元,且商场要完成不少于
元,且商场要完成不少于![]() 件的销售
件的销售
任务,则商场销售该品牌童装获得的最大利润是多少元?
![]() 如果要使利润不低于
如果要使利润不低于![]() 元,那么销售单价应在什么取值范围内?
元,那么销售单价应在什么取值范围内?
【答案】(1)w=-20x2+2880x-94000;(2)该商场销售该品牌童装获得的最大利润是9500元;;(3)要使利润不低于![]() 元,那么销售单价应满足
元,那么销售单价应满足![]() .
.
【解析】
(1)根据题意写出函数关系式;(2)抓住题中的不等关系列出不等式组求出单价的取值范围,再根据一次函数的增减性求利润最大值;(3)根据题意列出不等式求单价的取值范围.
(1)w=(x-50)[280+(80-x)×20]
=(x-50)(1880-20x)
=-20x2+2880x-94000;
(2)由题意,得![]() ,
,
解得:75≤x≤77,
由①w=-20x2+2880x-94000,
∵对称轴是直线x=72,-20<0,
∴当x>72时,w随x增大而减少.
又∵75≤x≤77,
∴当x=75时,w最大=-20×752+2880×75-94000=9500(元),
答:该商场销售该品牌童装获得的最大利润是9500元;
(3)根据题意可得-20x2+2880x-94000≥6800,
解得:60≤x≤84,
又∵50≤x≤80,
∴60≤x≤80,
答:要使利润不低于6800元,那么销售单价应满足60≤x≤80.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在下面的网格图中按要求画出图形,并回答问题:
(1)先画出△ABC向下平移5格后的△A1B1C1,再画出△ABC以点O为旋转中心,沿逆时针方向旋转90°后得到的△A2B2C2;
(2)如图,以点O为原点建立平面直角坐标系,试写出点A2,B1的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
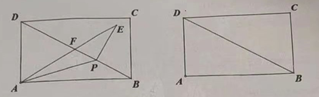
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为对角线
为对角线![]() 上异于点
上异于点![]() 的一个动点,联结
的一个动点,联结![]() ,将
,将![]() 沿
沿![]() 所在的直线翻折,使得点
所在的直线翻折,使得点![]() 落在点
落在点![]() 的位置
的位置
(1)当![]() 时,求点
时,求点![]() 到直线
到直线![]() 的距离。
的距离。
(2)联结![]() 交
交![]() 于
于![]() ,求当
,求当![]() 和
和![]() 相似时,线段
相似时,线段![]() 的长。
的长。
(3)当![]() 时,请直接写出此时
时,请直接写出此时![]() 的面积。
的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知y=(m2+m)![]() +(m﹣3)x+m2是x的二次函数,求出它的解析式.
+(m﹣3)x+m2是x的二次函数,求出它的解析式.
(2)用配方法求二次函数y=﹣x2+5x﹣7的顶点坐标并求出函数的最大值或最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数![]() 的图象的一部分,图象过点
的图象的一部分,图象过点![]() ,对称轴是直线
,对称轴是直线![]() ,给出五个结论:①
,给出五个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() .其中正确的是________(把你认为正确的序号都填上,答案格式如:“
.其中正确的是________(把你认为正确的序号都填上,答案格式如:“![]() ”).
”).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DEB中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是

A.BC=EC,∠B=∠E B.BC=EC,AC=DC
C.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形纸片ABCD中,已知AD=8,AB=6,E是边BC上的点,以AE为折痕折叠纸片,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com