Question

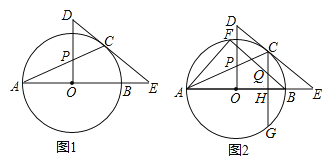
【题目】如图1，AB是⊙O的直径，E是AB延长线上一点，EC切⊙O于点C，OP⊥AO交AC于点P，交EC的延长线于点D．

（1）求证：△PCD是等腰三角形；

（2）CG⊥AB于H点，交⊙O于G点，过B点作BF∥EC，交⊙O于点F，交CG于Q点，连接AF，如图2，若sinE=，CQ=5，求AF的值．

Answer 1

【答案】（1）证明见解析；（2）12．

【解析】

试题分析：（1）连接OC，由切线性质和垂直性质得∠1+∠3=90°、∠2+∠4=90°，继而可得∠3=∠5得证；

（2）连接OC、BC，先根据切线性质和平行线性质及垂直性质证∠BCG=∠QBC得QC=QB=5，而sinE=sin∠ABF=，可知QH=3、BH=4，设圆的半径为r，在RT在△OCH中根据勾股定理可得r的值，在RT△ABF中根据三角函数可得答案．

试题解析：（1）连接OC，∵EC切⊙O于点C，∴OC⊥DE，∴∠1+∠3=90°，又∵OP⊥OA，∴∠2+∠4=90°，∵OA=OC，∴∠1=∠2，∴∠3=∠4，又∵∠4=∠5，∴∠3=∠5，∴DP=DC，即△PCD为等腰三角形；

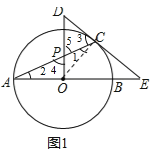
（2）如图2，连接OC、BC．∵DE与⊙O相切于点E，∴∠OCB+∠BCE=90°，∵OC=OB，∴∠OCB=∠OBC，∴∠OBC+∠BCE=90°，又∵CG⊥AB，∴∠OBC+∠BCG=90°，∴∠BCE=∠BCG，∵BF∥DE，∴∠BCE=∠QBC，∴∠BCG=∠QBC，∴QC=QB=5，∵BF∥DE，∴∠ABF=∠E，∵sinE=，∴sin∠ABF=，∴QH=3、BH=4，设⊙O的半径为r，∴在△OCH中，，解得：r=10，又∵∠AFB=90°，sin∠ABF=，∴AF=12．