
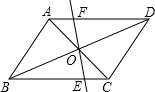
如图,![]() ABCD中,AC与BD的和为28,CD=5.(1)求△COD的周长;(2)△AOB、△BOC、△COD、△DOA的面积相等吗?为什么?若
ABCD中,AC与BD的和为28,CD=5.(1)求△COD的周长;(2)△AOB、△BOC、△COD、△DOA的面积相等吗?为什么?若![]() ABCD的面积是56,则△AOB的面积等于多少?(3)△ACD与△BCD的面积相等吗?为什么?
ABCD的面积是56,则△AOB的面积等于多少?(3)△ACD与△BCD的面积相等吗?为什么?

|
解:(1)由于在 AO=OC,BO=OD,且AC+BD=28 所以:CO+OD=14 又因为CD=5 所以:△COD的周长为19 (2)△AOB、△BOC、△COD、△DOA的面积相等.其理由是: S△ABO=S△ADO 用同样的方法,可得 S△ADO=S△CDO=S△BOC 即:S△AOB=S△BOC=S△COD=S△AOD 亦即:△AOB、△BOC、△COD、△DOA的面积相等. 又由于S 所以:4S△AOB=56 即:S△AOB=14 亦即:△AOB的面积为14. (3)方法一:由(2)可知S△AOD=S△COD=S△BOC 所以:S△AOD+S△DOC=S△BOC+S△DOC 所以:S△ACD=S△BCD 即:△ACD与△BCD的面积相等. 方法二:由于 所以:△ACD与△BCD的边CD上的高相等. 所以:S△ACD=S△BCD 即:△ACD与△BCD的面积相等. |
|
思路与技巧:(1)要求△COD的周长,一般思路是先求出CO、DO、CD这三条边的长(其中CD是已知的),但本题中由已知条件(AC与BD的和为28以及CD=5),不难分别求出CO、OD的长.事实上我们可根据“平行四边形对角线互相干分”,再利用“整体思想”可求出CO+OD,从而解决问题;(2)观察△AOB与△AOD,它们有相同的高,相等的底边(OB=OD),可得S△ABO=S△ADO(注:S△ABO表示△ABO的面积,以下相同.),依此类推:S△ADO=S△CDO=S△BCO;(3)两种思路:第一种思路是根据(2)中的结论:S△AOD=S△COD=S△BOC,可得到S△AOD+S△COD=S△BOC+S△COD,即S△ACD=S△BCD,第二种思路是观察到△ACD与△BCD有相同的底边CD,要说明二者面积相等,只需二者CD边上的高相等就可以了.事实上,这两条高恰好是两平行线AB与CD之间的距离,显然相等,故可以得到S△ACD=S△BCD. |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
 如图,?ABCD中,AB⊥AC,AB=1,BC=
如图,?ABCD中,AB⊥AC,AB=1,BC=| 5 |
| A、当旋转角为90°时,四边形ABEF一定为平行四边形 |
| B、在旋转的过程中,线段AF与EC总相等 |
| C、当旋转角为45°时,四边形BEDF一定为菱形 |
| D、当旋转角为45°时,四边形ABEF一定为等腰梯形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com