
 如图,大半圆O与小半圆O1相切于点C,大半圆的弦AB与小半圆相切与F,且AB∥CD,AB=4cm,则阴影部分的面积为2πcm2.
如图,大半圆O与小半圆O1相切于点C,大半圆的弦AB与小半圆相切与F,且AB∥CD,AB=4cm,则阴影部分的面积为2πcm2. 分析 作OH⊥AB于H,连接O1F,OB,如图,利用垂径定理得AH=BH=$\frac{1}{2}$AB=2,再根据切线的性质得O1F⊥AB,接着证明四边形OHFO1为矩形得到O1F=OH,利用圆的面积公式得到阴影部分的面积=$\frac{1}{2}$•π•(OB2-OH2),然后利用勾股定理得到OB2-OH2=BH2=4,于是得到阴影部分的面积=2π.
解答 解:作OH⊥AB于H,连接O1F,OB,如图,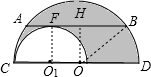 ∵OH⊥AB,
∵OH⊥AB,
∴AH=BH=$\frac{1}{2}$AB=2,
∵大半圆的弦AB与小半圆相切与F,
∴O1F⊥AB,
∵AB∥CD,
∴四边形OHFO1为矩形,
∴O1F=OH,
∵阴影部分的面积=$\frac{1}{2}$•π•OB2-$\frac{1}{2}$•π•O1F2
=$\frac{1}{2}$•π•(OB2-OH2)
而OB2-OH2=BH2=4,
∴阴影部分的面积=$\frac{1}{2}$•π•4=2π(cm2).
故答案为2πcm2.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.


科目:初中数学 来源: 题型:解答题
| 抛物线 | 开口方向 | 顶点坐标 | 对称轴 |
| y=3(x-2)2+4 | 向上 | (2,4) | x=2 |
| y=(x+2)2 | 向上 | (-2,0) | x=-2 |
| y=-$\frac{1}{3}{x}^{2}$+5 | 向下 | (0,5) | x=0 |
| y=y=$\frac{1}{6}(x+3)^{2}+1$ | $\frac{1}{6}(x+3)^{2}+1$向下 | (-3,1) | x=-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=ax2+bx+c经过点A(-1,2),顶点C的坐标为(1,-2),与y轴的交点为点B.
如图,抛物线y=ax2+bx+c经过点A(-1,2),顶点C的坐标为(1,-2),与y轴的交点为点B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com