
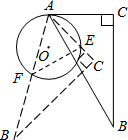
 如图,点A在⊙O上,⊙O的直径为8,∠B=30°,∠C=90°,AC=8.将△ABC从AC与⊙O相切于点A的位置开始,绕着点A顺时针旋转,旋转角为β(0°<β<120°),旋转后AC,AB分别与⊙O交于点E,F,连接EF.当BC与⊙O相切时,①旋转角β=________度;②△AEF的面积为________.
如图,点A在⊙O上,⊙O的直径为8,∠B=30°,∠C=90°,AC=8.将△ABC从AC与⊙O相切于点A的位置开始,绕着点A顺时针旋转,旋转角为β(0°<β<120°),旋转后AC,AB分别与⊙O交于点E,F,连接EF.当BC与⊙O相切时,①旋转角β=________度;②△AEF的面积为________.
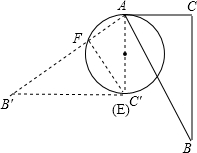 解:设旋转以后BC与⊙O相切于点H,则连接OH,OA,则OH⊥BC,则OA=OH=4,AC=8,因而OA+OH=AC,
解:设旋转以后BC与⊙O相切于点H,则连接OH,OA,则OH⊥BC,则OA=OH=4,AC=8,因而OA+OH=AC, AC′=4,
AC′=4, AC′=4
AC′=4 ,
, AF•FC′=
AF•FC′= ×4×4
×4×4 =8
=8 .
. .
.

科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
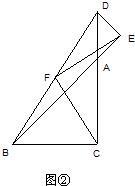
 如图,点D在AB上,直线DG交AF于点E.请从①DG∥AC,②AF平分∠BAC,③AD=DE中任选两个作为条件,余下一个作为结论,构造一个真命题,并说明理由.已知:
如图,点D在AB上,直线DG交AF于点E.请从①DG∥AC,②AF平分∠BAC,③AD=DE中任选两个作为条件,余下一个作为结论,构造一个真命题,并说明理由.已知:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com