
【题目】如图,在![]() 中,
中, ![]() ,点
,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,
上, ![]() ,连接
,连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 后得
后得![]() ,连接
,连接![]() .
.
(![]() )求证:
)求证: ![]() ≌
≌![]() .
.
(![]() )若
)若![]() ,求
,求![]() 的度数.
的度数.
【答案】(![]() )答案见解析.(
)答案见解析.(![]() )
)![]() .
.
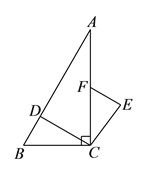
【解析】试题分析:(1)由旋转的性质可得:CD=CE,再根据同角的余角相等可证明∠BCD=∠FCE,再根据全等三角形的判定方法即可证明△BCD≌△FCE;
(2)由(1)可知:△BCD≌△FCE,所以∠BDC=∠E,易求∠E=90°,进而可求出∠BDC的度数.
试题解析:解:(1)∵将线段CD绕点C按顺时针方向旋转90°后得CE,∴CD=CE,∠DCE=90°,∵∠ACB=90°,∴∠BCD=90°﹣∠ACD=∠FCE,在△BCD和△FCE中,∵CB=CF,∠BCD=∠FCE,CD=CE,∴△BCD≌△FCE(SAS).
(2)由(1)可知△BCD≌△FCE,∴∠BDC=∠E,∠BCD=∠FCE,∴∠DCE=∠DCA+∠FCE=∠DCA+∠BCD=∠ACB=90°,∵EF∥CD,∴∠E=180°﹣∠DCE=90°,∴∠BDC=90°.


科目:初中数学 来源: 题型:
【题目】为了预防流感,某学校在休息天用药薰消毒法对教室进行消毒.已知药物释放过程中,室内每立方米空气中含药量y(毫克)与时间x(分钟)成正比例;药物释放完毕后,y与x成反比例,如图所示.根据图中提供的信息,解答下列问题:
(1)写出从药物释放开始,y与x之间的两个函数关系式及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量降低到0.45毫克以下时,学生方可进入教室,那么从药物释放开始,至少需要经过多少小时后,学生才能进入教室?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学举行“中国梦校园好声音”歌手大赛,初、高中部根据初赛成绩,各选出5名选手组成初中代表队和告知给你代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.
(1)根据图示填写表格;
平均数/分 | 中位数/分 | 众数/分 | |
初中代表队 | |||
高中代表队 |
(2)计算两队决赛成绩的方差,并判断哪一个代表队选手成绩较为稳定.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,M、N分别是AD、BC的中点,P、Q分别是BM、DN的中点.
(1)求证:△MBA≌△NDC;
(2)四边形MPNQ是什么样的特殊四边形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD⊥AB,EF⊥AB,垂足分别为D、F,∠1=∠2,
(1)试判断DG与BC的位置关系,并说明理由.
(2)若∠A=70°,∠BCG=40°,求∠AGD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】动物学家通过大量的调查估计出,某种动物活到20岁的概率为0.8,活到25岁的概率是0.5,活到30岁的概率是0.3.现年20岁的这种动物活到25岁的概率为多少?现年25岁的这种动物活到30岁的概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
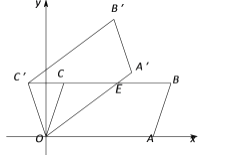
【题目】如图,在平面直角坐标系xOy中,平行四边形OABC的顶点A,B的坐标分别为(6,0),(7,3),将平行四边形OABC绕点O逆时针方向旋转得到平行四边形OA′B′C′,当点C′落在BC的延长线上时,线段OA′交BC于点E,则线段C′E的长度为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)等腰三角形一腰上的中线将这个等腰三角形的周长分成15 cm和6 cm两部分.求等腰三角形的底边长.

(2)已知等腰三角形中,有一个角比另一个角的2倍少20°,求顶角的度数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com