
(本题满分12分)如图,以点P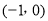 为圆心的圆,交x轴于B、C两点(B在C的左侧),交y轴于A、D两点(A在D的下方),AD=
为圆心的圆,交x轴于B、C两点(B在C的左侧),交y轴于A、D两点(A在D的下方),AD= ,将△ABC绕点P旋转180°,得到△MCB.
,将△ABC绕点P旋转180°,得到△MCB.

(1)求B、C两点的坐标;
(2)请在图中画出线段MB、MC,并判断四边形ACMB的形状(不必证明),求出点M的坐标;
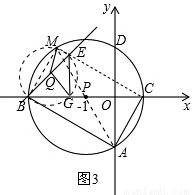
(3)动直线l从与BM重合的位置开始绕点B顺时针旋转,到与BC重合时停止,设直线l与CM交点为E,点Q为BE的中点,过点E作EG⊥BC于G,连接MQ、QG.请问在旋转过程中∠MQG的大小是否变化?若不变,求出∠MQG的度数;若变化,请说明理由.
(1)B(﹣3,0),C(1,0);(2)矩形,M(﹣2,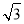 );(3)不变,∠MQG=120°.
);(3)不变,∠MQG=120°.
【解析】
试题分析:(1)连接PA,运用垂径定理及勾股定理即可求出圆的半径,从而可以求出B、C两点的坐标.
(2)由于圆P是中心对称图形,显然射线AP与圆P的交点就是所需画的点M,连接MB、MC即可;易证四边形ACMB是矩形;过点M作MH⊥BC,垂足为H,易证△MHP≌△AOP,从而求出MH、OH的长,进而得到点M的坐标.
(3)易证点E、M、B、G在以点Q为圆心,QB为半径的圆上,从而得到∠MQG=2∠MBG.易得∠OCA=60°,从而得到∠MBG=60°,进而得到∠MQG=120°,所以∠MQG是定值.
试题解析:(1)连接PA,如图1所示.
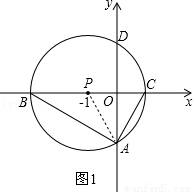
∵PO⊥AD,∴AO=DO.
∵AD=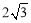 ,∴OA=
,∴OA=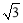 .
.
∵点P坐标为(﹣1,0),∴OP=1.∴PA=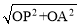 =2.∴BP=CP=2.∴B(﹣3,0),C(1,0).
=2.∴BP=CP=2.∴B(﹣3,0),C(1,0).
(2)连接AP,延长AP交⊙P于点M,连接MB、MC.如图2所示,线段MB、MC即为所求作.
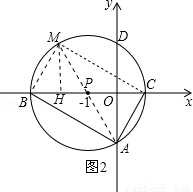
四边形ACMB是矩形.理由如下:
∵△MCB由△ABC绕点P旋转180°所得,∴四边形ACMB是平行四边形.
∵BC是⊙P的直径,∴∠CAB=90°.∴平行四边形ACMB是矩形.
过点M作MH⊥BC,垂足为H,如图2所示.
在△MHP和△AOP中,
∵∠MHP=∠AOP,∠HPM=∠OPA,MP=AP,∴△MHP≌△AOP.∴MH=OA=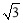 ,PH=PO=1.
,PH=PO=1.
∴OH=2.∴点M的坐标为(﹣2,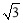 ).
).
(3)在旋转过程中∠MQG的大小不变.
∵四边形ACMB是矩形,∴∠BMC=90°.
∵EG⊥BO,∴∠BGE=90°.∴∠BMC=∠BGE=90°.
∵点Q是BE的中点,∴QM=QE=QB=QG.∴点E、M、B、G在以点Q为圆心,QB为半径的圆上,如图3所示.∴∠MQG=2∠MBG.
∵∠COA=90°,OC=1,OA=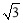 ,∴tan∠OCA=
,∴tan∠OCA=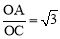 .∴∠OCA=60°.∴∠MBC=∠BCA=60°.
.∴∠OCA=60°.∴∠MBC=∠BCA=60°.
∴∠MQG=120°.
∴在旋转过程中∠MQG的大小不变,始终等于120°.
考点:圆的综合题.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:初中数学 来源:2014-2015学年江苏省江阴市华士片九年级上学期期中考试数学试卷(解析版) 题型:选择题
已知关于x的一元二次方程 有两个不相等的实数根,则a的取值
有两个不相等的实数根,则a的取值
范围是( )
A.a<2 B.a>2 C.a<2且a≠1 D.a<-2
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市华士片七年级上学期期中考试数学试卷(解析版) 题型:填空题
江苏省的面积约为102 600km2,这个数据用科学记数法可表示为 km2.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市华士片七年级上学期期中考试数学试卷(解析版) 题型:选择题
有理数 、
、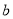 在数轴上的位置如图所示,则下列正确的是( )
在数轴上的位置如图所示,则下列正确的是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江都市九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分10分) 如图,某农场老板准备建造一个矩形羊圈ABCD,他打算让矩形羊圈的一面完全靠着墙MN,墙MN可利用的长度为25m,另外三面用长度为50m的篱笆围成(篱笆正好要全部用完,且不考虑接头的部分).

(1)若要使矩形羊圈的面积为300m2,则垂直于墙的一边长AB为多少米?
(2)农场老板又想将羊圈ABCD的面积重新建造成面积为320 ,从而可以养更多的羊,请聪明的你告诉他:他的这个想法能实现吗?为什么?
,从而可以养更多的羊,请聪明的你告诉他:他的这个想法能实现吗?为什么?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江都市九年级上学期期中考试数学试卷(解析版) 题型:填空题
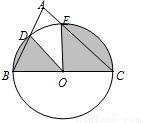
如图,以BC为直径的⊙O与△ABC的另两边分别相交于点D、E.若∠A=70°,BC=2,则图中阴影部分面积为 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省八年级上学期期中联考数学试卷(解析版) 题型:解答题
某园艺公司对一块直角三角形的花圃进行改造,测得两直角边长分别为6 m、8 m.现要将其扩建成等腰三角形,且扩充部分是以8 m为一个直角边长的直角三角形.请在下面三张图上分别画出三种不同的扩建后的图形,并求出扩建后的等腰三角形花圃的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com