
 如图,在平行四边形ABCD中,AB=6,AD=8,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于G,BG=4$\sqrt{2}$,则四边形AECD的周长为( )
如图,在平行四边形ABCD中,AB=6,AD=8,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于G,BG=4$\sqrt{2}$,则四边形AECD的周长为( )| A. | 20 | B. | 21 | C. | 22 | D. | 23 |
分析 由在?ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,易得△ABE是等腰三角形,继而求得BE与CE的长,又由BG⊥AE于G,BG=4$\sqrt{2}$,即可求得AE的长,继而求得答案.
解答 解:∵四边形ABCD是平行四边形,
∴BC=AD=9,CD=AB=6,AD∥BC,
∴∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠DAE=∠BAE,
∴∠BAE=∠BEA,
∴BE=AB=6,
∴EC=BC-BE=3,
∵BG⊥AE,
∴AG=EG=$\sqrt{A{B}^{2}-B{G}^{2}}$=$\sqrt{{6}^{2}-(4\sqrt{2})^{2}}$=2,
∴AE=AG+EG=4,
∴四边形AECD的周长为:AD+CD+CE+AE=9+6+3+4=22.
故选:C.
点评 此题考查了平行四边形的性质、等腰三角形的判定与性质以及勾股定理.此题难度适中,注意掌握数形结合思想的应用.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 矩形的对角线互相平分且相等 | |
| B. | 对角线互相垂直的四边形是菱形 | |
| C. | 四个角都相等的四边形是矩形 | |
| D. | 两组对边分别相等的四边形是平行四边形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
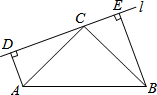 如图,在Rt△ABC中,∠ACB=90°,AC=BC,过C点作直线l,点 D,E在直线l上,连接AD,BE,∠ADC=∠CEB=90°.求证:△ADC≌△CEB.
如图,在Rt△ABC中,∠ACB=90°,AC=BC,过C点作直线l,点 D,E在直线l上,连接AD,BE,∠ADC=∠CEB=90°.求证:△ADC≌△CEB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明所在数学兴趣小组,计划用尺规作图作直角三角形,且这个直角三角形的一条边为2倍的单位长度,另一条边为4倍的单位长度.
小明所在数学兴趣小组,计划用尺规作图作直角三角形,且这个直角三角形的一条边为2倍的单位长度,另一条边为4倍的单位长度.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,∠AOB=∠COD=90°,OE平分∠BOD,若∠AOD:∠BOC=5:1,则∠COE的度数为( )
如图,∠AOB=∠COD=90°,OE平分∠BOD,若∠AOD:∠BOC=5:1,则∠COE的度数为( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com