
【题目】如图,在△ABC中,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得到△CFE . 
(1)求证:四边形ADCF是平行四边形.
(2)当△ABC满足什么条件时,四边形ADCF是正方形?请说明理由.
【答案】
(1)
解答:证明:∵△CFE是由△ADE绕点E旋转180°得到,
∴点A、E、C三点共线,点D、E、F三点共线,且AE=CE,DE=FE,故四边形ADCF是平行四边形.
(2)
解答:解:当∠ACB=90°,AC=BC时,四边形ADCF是正方形.
理由如下:在△ABC中,∵AC=BC,AD=BD,点D是边AB的中点,
∴CD⊥AB,即∠ADC=90°,
而由(1)知,四边形ADCF是平行四边形,
∴四边形ADCF是矩形.
又∵∠ACB=90°,
∴CD= ![]() AB=AD,
AB=AD,
故四边形ADCF是正方形.
【解析】(1)利用旋转的性质得出点A、E、C三点共线,点D、E、F三点共线,且AE=CD , DE=FE , 即可得出答案;(2)首先得出CD⊥AB , 即∠ADC=90°,由(1)知,四边形ADCF是平行四边形,故四边形ADCF是矩形.进而求出CD=AD即可得出答案.
【考点精析】本题主要考查了平行四边形的判定和正方形的判定方法的相关知识点,需要掌握两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形;先判定一个四边形是矩形,再判定出有一组邻边相等;先判定一个四边形是菱形,再判定出有一个角是直角才能正确解答此题.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
(1)整式2xy﹣8x2y+8x3y因式分解的结果是2xy(1﹣4x+4x2);
(2)要使y=![]() 有意义,则x应该满足0<x≤3;
有意义,则x应该满足0<x≤3;
(3)“x的2倍与5的和”用代数式表示是一次式;
(4)地球上的陆地面积约为149000000平方千米,用科学记数法表示为1.49×108平方千米.
A.(1)(4)
B.(1)(2)
C.(2)(3)
D.(3)(4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学在作业中的计算摘录:①a0=1;②a2a3=a5;③2﹣2=﹣![]() ;④(﹣3x2y)3(xy)3=﹣27x9y6;
;④(﹣3x2y)3(xy)3=﹣27x9y6;
⑤x2+x2=2x2;⑥(a2b)3=a2b3;⑦(﹣bc)4÷(﹣bc)2=b2c2 . 其中计算正确的是( )
A.①②③④
B.①③⑤⑦
C.②③④⑥
D.②④⑤⑦
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠B=∠C=90°,∠CED=35°,DE平分∠ADC. 
(1)求∠DAB的度数;
(2)若E为BC中点,求∠EAB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线m,n相交于点B,点A,C分别为直线m,n上的点,AB=BC=1,且∠ABC=60°,点E是直线m上的一个动点,点D是直线n上的一个动点,运动过程中始终满足DE=CE. 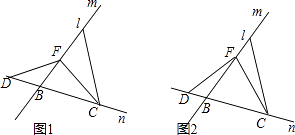
(1)如图1,当点E运动到线段AB的中点,点D在线段CB的延长线上时,求BD的长.
(2)如图2,当点E在线段AB上运动,点D在线段CB的延长线上时,试确定线段BD与AE的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
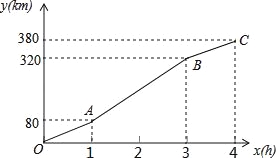
【题目】暑假期间,小刚一家乘车去离家380公里的某景区旅游,他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象如图所示.
(1)从小刚家到该景区乘车一共用了多少时间?
(2)求线段AB对应的函数解析式;
(3)小刚一家出发2.5小时时离目的地多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有铅笔、练习本、圆珠笔三种学习用品,若购铅笔3支、练习本7本、圆珠笔1支共需6.3元;若购铅笔4支、练习本10本、圆珠笔1支共需8.4元.现购铅笔、圆珠笔各1支、练习本1本,共需( )元.
A.2.4
B.2.1
C.1.9
D.1.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校大课间活动中,小英、小丽和小敏在操场上画出A、B两个区域,一起玩投沙包游戏,沙包落在A区域所得分值与落在B区域所得分值不同,当每个各投沙包四次时,其落点和四次总分如图所示.
(1)请求出A区域和B区域每个沙包落点的分值分别是多少?
(2)求小敏的得分
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com