
【题目】已知直线m,n相交于点B,点A,C分别为直线m,n上的点,AB=BC=1,且∠ABC=60°,点E是直线m上的一个动点,点D是直线n上的一个动点,运动过程中始终满足DE=CE. 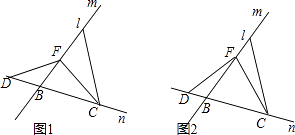
(1)如图1,当点E运动到线段AB的中点,点D在线段CB的延长线上时,求BD的长.
(2)如图2,当点E在线段AB上运动,点D在线段CB的延长线上时,试确定线段BD与AE的数量关系,并说明理由.
【答案】
(1)解:∵∠ABC=60°,AB=BC,
∴△ABC为等边三角形,
∴∠ACB=60°,
∵点E是线段AB的中点,
∴∠ECB= ![]() ∠ACB=30°,
∠ACB=30°,
∵DE=CE,
∴∠EDB=∠ECB=30°,
∵∠ABC=∠EDB+∠DEB,
∴∠DEB=30°=∠EDB,
∴BD=DE= ![]() AB=
AB= ![]()
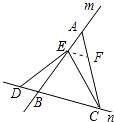
(2)解:BD=AE;理由如下:
过点E作EF∥BC交AC于点F,如图所示:
∵EF∥BC,
∴∠AFE=∠ACB=60°,
∴∠EFC=120°,∠AFE=∠A,
∴EF=EA,
∵∠ABC=60°,
∴∠EBD=120°,
∴∠EFC=∠EBD,
∵CE=DE,
∴∠EDB=∠ECB,
∵∠EDB+∠DEB=∠ECB+∠ECF=60°,
∴∠DEB=∠ECF,
在△EDB和△CEF中, 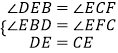 ,
,
∴△EDB≌△CEF(AAS),
∴BD=EF,
∵EF=EA,
∴BD=AE.
【解析】(1)证明△ABC为等边三角形,得出∠ACB=∠ABC=60°,由等边三角形的性质得出∠ECB= ![]() ∠ACB=30°,由等腰三角形的性质得出∠EDB=30°,由三角形的外角性质得出∠DEB=∠EDB,即可得出结论;(2过点E作EF∥BC交AC于点F,由平行线的性质得出∠AFE=∠ACB=60°,证出∠EFC=120°,∠AFE=∠A,得出EF=EA,证出∠DEB=∠ECF,由AAS证明△EDB≌△CEF,得出BD=EF,即可得出结论.
∠ACB=30°,由等腰三角形的性质得出∠EDB=30°,由三角形的外角性质得出∠DEB=∠EDB,即可得出结论;(2过点E作EF∥BC交AC于点F,由平行线的性质得出∠AFE=∠ACB=60°,证出∠EFC=120°,∠AFE=∠A,得出EF=EA,证出∠DEB=∠ECF,由AAS证明△EDB≌△CEF,得出BD=EF,即可得出结论.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】某市计划进行一项城市美化工程,已知乙队单独完成此项工程比甲队单独完成此项工程多用10天,且甲队单独施工30天和乙队单独施工45天的工作量相同.
(1)甲、乙两队单独完成此项工程各需多少天?
(2)已知甲队每天的施工费用为8000元,乙队每天的施工费用为6000元,为了缩短工期,指挥部决定该工程由甲、乙两队一起来完成,则该工程施工费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得到△CFE . 
(1)求证:四边形ADCF是平行四边形.
(2)当△ABC满足什么条件时,四边形ADCF是正方形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是边长为4cm的正方形ABCD的中心,M是BC的中点,动点P由A开始沿折线A—B—M方向匀速运动,到M时停止运动,速度为1cm/s. 设P点的运动时间为t(s),点P的运动路径与OA、OP所围成的图形面积为S(cm2),则描述面积S(cm2)与时间t(s)的关系的图像可以是( )
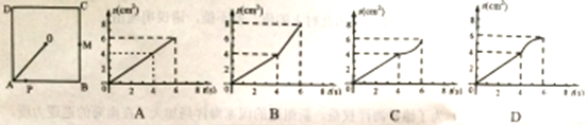
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将抛物线y=2(x﹣3)2﹣2绕它的顶点旋转180°,所得抛物线的解析式是( )
A.y=﹣2(x﹣3)2+2B.y=﹣2(x+3)2+2
C.y=﹣2(x﹣3)2﹣2D.y=﹣2(x+3)2﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点O在AB边上,过点O作BC的平行线交∠ABC的平分线于点D , 过点B作BE⊥BD交直线OD于点E . 
(1)求证:OE=OD;
(2)当点O在AB的什么位置时,四边形BDAE是矩形?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com