
【题目】如图,在△ABC中,点O在AB边上,过点O作BC的平行线交∠ABC的平分线于点D , 过点B作BE⊥BD交直线OD于点E . 
(1)求证:OE=OD;
(2)当点O在AB的什么位置时,四边形BDAE是矩形?说明理由.
【答案】
(1)
解答:证明:∵BD是∠ABC的角平分线,
∴∠ABD=∠DBC;∵ED∥BC,
∴∠ODB=∠DBC=∠ABD,
∴△OBD为等腰三角形,
∴OB=OD,在Rt△EBD中,OB=OD,那么O就是斜边ED的中点.
∴OE=OD.
(2)
解答:O为AB的中点时,四边形BDAE为矩形
∵四边形BDAE为矩形,
∴∠AEB为直角即△AEB为直角三角形,OA=OB=OE=OD,
∵Rt△AEB中,OE=OA=OB,
∴O为斜边AB的中点,
∴O为AB的中点时,四边形BDAE为矩形.
【解析】(1)根据角平分线和等腰三角形腰长相等性质证明OB=OD , 再根据直角三角形中线的性质即可判定O点为DE的中点,即OE=OD;(2)设定四边形BDAE为矩形,可求出Rt△AEB中,O点为斜边AB的中点.
【考点精析】通过灵活运用直角三角形斜边上的中线和矩形的判定方法,掌握直角三角形斜边上的中线等于斜边的一半;有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形即可以解答此题.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】已知直线m,n相交于点B,点A,C分别为直线m,n上的点,AB=BC=1,且∠ABC=60°,点E是直线m上的一个动点,点D是直线n上的一个动点,运动过程中始终满足DE=CE. 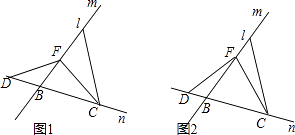
(1)如图1,当点E运动到线段AB的中点,点D在线段CB的延长线上时,求BD的长.
(2)如图2,当点E在线段AB上运动,点D在线段CB的延长线上时,试确定线段BD与AE的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店中销售水果时采用了三种组合搭配的方式进行销售,甲种搭配是:2千克A水果,4千克B水果;乙种搭配是:3千克A水果,8千克B水果,1千克C水果;丙种搭配是:2千克A水果,6千克B水果,1千克C水果;如果A水果每千克售价为2元,B水果每千克售价为1.2元,C水果每千克售价为10元,某天,商店采用三种组合搭配的方式进行销售后共得销售额441.2元,并且A水果销售额116元,那么C水果的销售额是元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC , 点D(不与点B重合)在BC上,点E是AB的中点,过点A作AF∥BC交DE延长线于点F , 连接AD , BF . 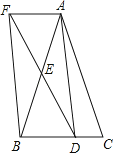
(1)求证:△AEF≌△BED;
(2)若BD=CD , 求证:四边形AFBD是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校大课间活动中,小英、小丽和小敏在操场上画出A、B两个区域,一起玩投沙包游戏,沙包落在A区域所得分值与落在B区域所得分值不同,当每个各投沙包四次时,其落点和四次总分如图所示.
(1)请求出A区域和B区域每个沙包落点的分值分别是多少?
(2)求小敏的得分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将△AOB绕原点O顺时针旋转180°后得到△A1OB1 , 若点B的坐标为(2,1),则点B的对应点B1的坐标为( )
A.(1,2)
B.(2,﹣1)
C.(﹣2,1)
D.(﹣2,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列变形属于移项的是( )
A. 由3x+2-2x=5,得3x-2x+2=5
B. 由3x+2x=1,得5x=1
C. 由2(x-1)=3,得2x-2=3
D. 由9x+5=-3,得9x=-3-5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com