
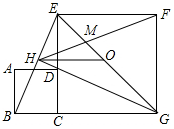
 如图,正方形ABCD的边CD在正方形ECGF的边CE上,O是EG的中点,∠EGC的平分线GH过点D,交BE于点H,连接OH,FH,EG与FH交于点M,对于下面四个结论:
如图,正方形ABCD的边CD在正方形ECGF的边CE上,O是EG的中点,∠EGC的平分线GH过点D,交BE于点H,连接OH,FH,EG与FH交于点M,对于下面四个结论:分析 证明△BCE≌△DCG,即可证得∠BEC=∠DGC,然后根据三角形的内角和定理证得∠EHG=90°,则HG⊥BE,然后证明△BGH≌△EGH,则H是BE的中点,则OH是△BGE的中位线,根据三角形的中位线定理即可得到HO=$\frac{1}{2}$BG,HO∥BG,以及∠MOH=∠EGC=45°,再根据等腰直角三角形的性质,得出OF=$\frac{1}{2}$EG,∠OFG=45°,以及OH=OF,根据∠MHO+∠HOM=∠OFH+∠OFG,即可得出∠FMG=∠MFG,最后根据等腰直角三角形的边角关系,得出DB:AB=$\sqrt{2}$:1,即可得到DE:AB=$\sqrt{2}$:1.
解答  解:∵正方形ABCD的边CD在正方形ECGF的边CE上,
解:∵正方形ABCD的边CD在正方形ECGF的边CE上,
∴∠BCE=∠DCG=90°,BC=DC,EC=GC,
∴△BCE≌△DCG(SAS),
∴∠CGD=∠CEB,
又∵∠CDG=∠HDE,
∴∠EHD=∠GCD=90°,
∴GH⊥BE,故①正确;
∵∠EGC的平分线GH过点D,
∴∠BGH=∠EGH,
∵GH⊥BE,
∴∠BHG=∠EHG=90°,
∴△BGH≌△EGH(ASA),
∴BG=EG,故②正确;
∵BG=EG,GH⊥BE,
∴H为BE的中点,
又∵O是EG的中点,
∴HO是△BEG的中位线,
∴HO=$\frac{1}{2}$BG,HO∥BG,
∴∠MOH=∠EGC=45°,
如图,连接FO,
∵O是EG的中点,
∴等腰Rt△EFG中,OF=$\frac{1}{2}$EG,∠OFG=45°,
∴OH=OF,
∴∠OHF=∠OFH,
∴∠MHO+∠HOM=∠OFH+∠OFG,即∠FMG=∠MFG,
∴FG=MG,即△MFG是等腰三角形,故③正确;
如图,连接BD,
∵HG垂直平分BE,
∴DE=DB,
∵Rt△ABD中,DB:AB=$\sqrt{2}$:1,
∴DE:AB=$\sqrt{2}$:1,故④错误;
故答案为:①②③
点评 本题主要考查了四边形的综合应用,解题时需要综合运用正方形的性质,三角形中位线定理,全等三角形的判定与性质,等腰直角三角形的性质以及等腰三角形的判定等,解题的关键是作辅助线构造等腰三角形和等腰直角三角形,灵活利用直角三角形的边角关系来计算.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
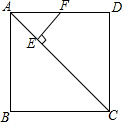 如图,正方形ABCD的边长为1,AC为其对角线,点E为AC上一点且满足CE=CD,过点E作EF⊥AC交AD于点F,则DF的长度为$\sqrt{2}$-1.
如图,正方形ABCD的边长为1,AC为其对角线,点E为AC上一点且满足CE=CD,过点E作EF⊥AC交AD于点F,则DF的长度为$\sqrt{2}$-1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
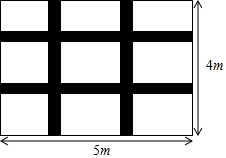 如图,一块长5米宽4米的地毯,为了美观设计了两横、两纵的配色条纹(图中阴影部分),已知配色条纹的宽度相同,所占面积是整个地毯面积的$\frac{17}{80}$.求配色条纹的宽度.
如图,一块长5米宽4米的地毯,为了美观设计了两横、两纵的配色条纹(图中阴影部分),已知配色条纹的宽度相同,所占面积是整个地毯面积的$\frac{17}{80}$.求配色条纹的宽度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com