
【题目】如图,在ABCD中,点E,M分别在边AB,CD上,且AE=CM,点F,N分别在边BC,AD上,且DN=BF. 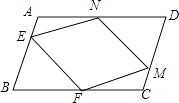
(1)求证:△AEN≌△CMF;
(2)连接EM,FN,若EM⊥FN,求证:EFMN是菱形.
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,∠A=∠C,
∵ND=BF,
∴AD﹣ND=BC﹣BF,
即AN=CF,
在△AEN和△CMF中
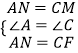 ,
,
∴△AEN≌△CMF(SAS)
(2)证明:如图:由(1)△AEN≌△CMF,
故EN=FM,
同理可得:△EBF≌△MDN,
∴EF=MN,
∵EN=FM,EF=MN,
∴四边形EFMN是平行四边形,
∵EM⊥FN,
∴四边形EFMN是菱形.

【解析】(1)直接利用平行四边形的性质得出AN=CF,再利用全等三角形的判定方法得出答案;(2)直接利用全等三角形的判定与性质得出EN=FM,EF=MN,再结合菱形的判定方法得出答案.
【考点精析】本题主要考查了平行四边形的性质和菱形的判定方法的相关知识点,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形才能正确解答此题.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:
【题目】两个一模一样的梯形纸片如图(1)摆放,将梯形纸片ABCD沿上底AD方向向右平移得到图(2).已知AD=4,BC=8,若阴影部分的面积是四边形A′B′CD的面积的 ![]() ,则图(2)中平移距离A′A=
,则图(2)中平移距离A′A=
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于函数y=-3x,判断正确的是( )
A. 图象经过点(0,0)和点(-1,-3)
B. 图象经过第一、三象限
C. y随x的增大而减小
D. 图象是一条射线
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点(-1,y1),(4,y2)在一次函数y=3x-2的图象上,则y1,y2,0的大小关系是( )
A. 0<y1<y2 B. y1<0<y2
C. y1<y2<0 D. y2<0<y1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线MN与直线PQ垂直相交于O,点A在直线PQ上运动,点B在直线MN上运动.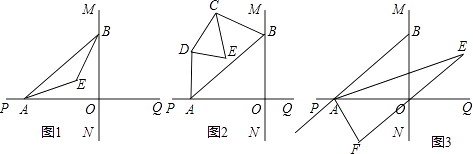
(1)如图1,已知AE、BE分别是∠BAO和∠ABO角的平分线,点A、B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠AEB的大小.
(2)如图2,已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,又DE、CE分别是∠ADC和∠BCD的角平分线,点A、B在运动的过程中,∠CED的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值.
(3)如图3,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及延长线相交于E、F,在△AEF中,如果有一个角是另一个角的3倍,试求∠ABO的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com