
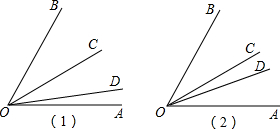
 解:分两种情况考虑:
解:分两种情况考虑: ∠AOB=36°,
∠AOB=36°, ∠AOC=12°,
∠AOC=12°, ∠AOC=12°,
∠AOC=12°,

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 |
| AB |
 |
| CB |
| CF |
| AF |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•枣阳市模拟)已知如图,矩形OABC的长OA=
(2012•枣阳市模拟)已知如图,矩形OABC的长OA=| 3 |
| 2 |
| 3 |
| 3 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
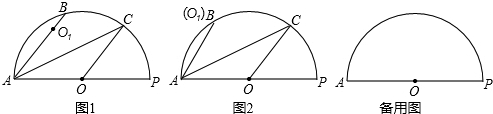
已知如图,矩形OABC的长OA=![]() ,宽OC=1,将△AOC沿AC翻折得△AFC.
,宽OC=1,将△AOC沿AC翻折得△AFC.
1.求过A、F、C三点的抛物线解析式;
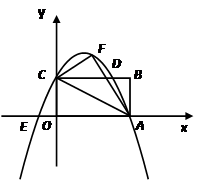
2.设(1)中的抛物线与矩形OABC边CB相交于点D,与![]() 轴相交于另外一点E,若点M是
轴相交于另外一点E,若点M是![]() 轴上的点,N是
轴上的点,N是![]() 轴上的点,若以点E、M、D、N为顶点的四边形是平行四边形,试求点M、N的坐标
轴上的点,若以点E、M、D、N为顶点的四边形是平行四边形,试求点M、N的坐标
3.若动点P以每秒![]() 个单位长度的速度从C点出发沿CB 向终点B运动,同时动点Q从A点出发以每秒
个单位长度的速度从C点出发沿CB 向终点B运动,同时动点Q从A点出发以每秒![]() 个单位长度的速度沿射线AO运动,当P运动到B点时,P,Q同时停止运动.当点P运动时间t(秒)为何值时,以P、C、O为顶点的三角形与以Q、O、C为顶点的三角形相似?
个单位长度的速度沿射线AO运动,当P运动到B点时,P,Q同时停止运动.当点P运动时间t(秒)为何值时,以P、C、O为顶点的三角形与以Q、O、C为顶点的三角形相似?
查看答案和解析>>
科目:初中数学 来源:2012届湖北省枣阳市中考模拟数学试卷(带解析) 题型:解答题
已知如图,矩形OABC的长OA=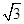 ,宽OC=1,将△AOC沿AC翻折得△AFC.
,宽OC=1,将△AOC沿AC翻折得△AFC.
【小题1】求过A、F、C三点的抛物线解析式;
【小题2】设(1)中的抛物线与矩形OABC边CB相交于点D,与 轴相交于另外一点E,若点M是
轴相交于另外一点E,若点M是 轴上的点,N是
轴上的点,N是 轴上的点,若以点E、M、D、N为顶点的四边形是平行四边形,试求点M、N的坐标
轴上的点,若以点E、M、D、N为顶点的四边形是平行四边形,试求点M、N的坐标
【小题3】若动点P以每秒 个单位长度的速度从C点出发沿CB 向终点B运动,同时动点Q从A点出发以每秒
个单位长度的速度从C点出发沿CB 向终点B运动,同时动点Q从A点出发以每秒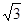 个单位长度的速度沿射线AO运动,当P运动到B点时,P,Q同时停止运动.当点P运动时间t(秒)为何值时,以P、C、O为顶点的三角形与以Q、O、C为顶点的三角形相似?
个单位长度的速度沿射线AO运动,当P运动到B点时,P,Q同时停止运动.当点P运动时间t(秒)为何值时,以P、C、O为顶点的三角形与以Q、O、C为顶点的三角形相似?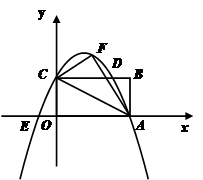
查看答案和解析>>
科目:初中数学 来源:2012年湖北省襄阳市枣阳市中考适应性考试数学试卷(解析版) 题型:解答题
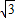 ,宽OC=1,将△AOC沿AC翻折得△AFC.
,宽OC=1,将△AOC沿AC翻折得△AFC.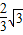 个单位长度的速度从C点出发沿CB 向终点B运动,同时动点Q从A点出发以每秒
个单位长度的速度从C点出发沿CB 向终点B运动,同时动点Q从A点出发以每秒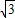 个单位长度的速度沿射线AO运动,当P运动到B点时,P,Q同时停止运动.当点P运动时间t(秒)为何值时,以P、C、O为顶点的三角形与以Q、O、C为顶点的三角形相似?
个单位长度的速度沿射线AO运动,当P运动到B点时,P,Q同时停止运动.当点P运动时间t(秒)为何值时,以P、C、O为顶点的三角形与以Q、O、C为顶点的三角形相似?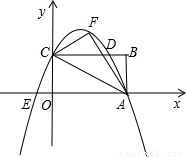
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com