
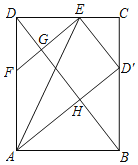
【题目】如图,在矩形ABCD中,E为CD上一点,若△ADE沿直线AE翻折,使点D落在BC边上点D′处.F为AD上一点,且DF=CD',EF与BD相交于点G,AD′与BD相交于点H.D′E∥BD,HG=4,则BD=__.
【答案】6+2![]() .
.
【解析】
由折叠的性质得AD′=AD,D′E=DE,∠ADE=∠AD′E=90°,证明△CD′E~△BAD′,得出![]() ,得出
,得出 ![]() ,证明△EDF∽△DAB,得出∠FED=∠ADB,证明四边形HGED′是矩形,得出∠GED'=90°,HG=ED′=DE=4,设EC=y,CD′=x,证明△DGE≌△ECD′(AAS),得出DG=CE=y,EG=CD′=HD′=x,同理△BHD′∽△D′CE,得出
,证明△EDF∽△DAB,得出∠FED=∠ADB,证明四边形HGED′是矩形,得出∠GED'=90°,HG=ED′=DE=4,设EC=y,CD′=x,证明△DGE≌△ECD′(AAS),得出DG=CE=y,EG=CD′=HD′=x,同理△BHD′∽△D′CE,得出 ![]() ,BH=
,BH=![]() ,BD=BH+GH+DG=y+4+
,BD=BH+GH+DG=y+4+ ![]() ,同理△DFE∽△CED′,得出
,同理△DFE∽△CED′,得出 ![]() ,得出x2=4y,由勾股定理得出x2+y2=16,得出y2+4y﹣16=0,解方程即可.
,得出x2=4y,由勾股定理得出x2+y2=16,得出y2+4y﹣16=0,解方程即可.
解:∵四边形ABCD是矩形,
∴∠C=∠ABD′=∠BAD=∠ADC=90°,
由折叠的性质得:AD′=AD,D′E=DE,∠ADE=∠AD′E=90°,
∴AD′⊥D′E,
∵D′E∥BD,
∴BD⊥AD′,
∴∠GHD′=∠HD′E=90°,
∴∠ED′C+∠BD′A=90°,
∵∠BAD′+∠BD′A=90°,
∴∠ED′C=∠BAD′,
∵∠C=∠ABD′,
∴△CD′E~△BAD′,
∴![]() ,
,
∵CD′=DF,
∴![]() ,
,
∵∠EDF=∠BAD=90°,
∴△EDF∽△DAB,
∴∠FED=∠ADB,
∵∠ADB+∠BDC=90°,
∴∠FED+∠BDC=90°,
∴∠DGE=90°,
∴∠GHD′=∠HD′E=∠HGE=90°,
∴四边形HGED′是矩形,
∴∠GED'=90°,HG=ED′=DE=4,
设EC=y,CD′=x,
∵∠DEG+∠D'EC=∠D'EC+∠CD'E=90°,
∴∠DEG=∠CD'E,
在△DGE和△ECD'中, ,
,
∴△DGE≌△ECD′(AAS),
∴DG=CE=y,EG=CD′=HD′=x,
同理△BHD′∽△D′CE,
∴![]() ,
,
∴![]() ,
,
∴BH=![]() ,
,
∴BD=BH+GH+DG=y+4+![]() ,
,
同理△DFE∽△CED′,
∴![]() ,
,
∴![]() ,
,
∴x2=4y,
∵x2+y2=16,
∴y2+4y﹣16=0,
∴y=﹣2+2![]() ,或y=﹣2﹣2
,或y=﹣2﹣2![]() (舍弃),
(舍弃),
∴BD=﹣2+2![]() +4+4=6+2
+4+4=6+2![]() ;
;
故答案为:6+2![]() .
.


科目:初中数学 来源: 题型:
【题目】苏北五市联合通过网络投票选出了一批“最有孝心的美少年”.根据各市的入选结果制作出如下统计表,后来发现,统计表中前三行的所有数据都是正确的,后两行中有一个数据是错误的.请回答下列问题:
(1)统计表![]() ________,
________,![]() ________;
________;
(2)统计表后三行中哪一个数据是错误的?该数据的正确值是多少?
(3)组委会决定从来自宿迁市的4位“最有孝心的美少年”中,任选两位作为苏北五市形象代言人,![]() 、
、![]() 是宿迁市“最有孝心的美少年”中的两位,问
是宿迁市“最有孝心的美少年”中的两位,问![]() 、
、![]() 同时入选的概率是多少?并请画出树状图或列出表格.
同时入选的概率是多少?并请画出树状图或列出表格.
区域 | 频数 | 频率 |
宿迁 | 4 | a |
连云港 | 7 | 0.175 |
淮安 |
| 0.2 |
徐州 | 10 | 0.25 |
盐城 | 12 | 0.275 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() .
.
(1)求抛物线![]() 的开口方向、对称轴和顶点坐标;
的开口方向、对称轴和顶点坐标;
(2)将抛物线![]() 向下平移,得抛物线
向下平移,得抛物线![]() ,使抛物线
,使抛物线![]() 的顶点落在直线
的顶点落在直线![]() 上.
上.
①求抛物线![]() 的解析式;
的解析式;
②抛物线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,
,![]() (点
(点![]() 在点
在点![]() 的左侧),抛物线
的左侧),抛物线![]() 的对称轴于
的对称轴于![]() 轴的交点为
轴的交点为![]() ,点
,点![]() 是线段
是线段![]() 上的一点,过点
上的一点,过点![]() 作直线
作直线![]() 轴,交抛物线
轴,交抛物线![]() 于点
于点![]() ,点
,点![]() 关于抛物线对称轴的对称点为
关于抛物线对称轴的对称点为![]() ,点
,点![]() 是线段
是线段![]() 上一点,且
上一点,且![]() ,连接
,连接![]() ,作
,作![]() 交
交![]() 轴于点
轴于点![]() ,且
,且![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅行团计划今年暑假组织一个老年人团去昆明旅游,预定宾馆住宿时,有住宿条件一样的甲、乙两家宾馆供选择,其收费标准为每人每天120元,并且各自推出不同的优惠方案.甲家是35人(含35人)以内的按标准收费,超过35人的,超出部分按九折收费;乙家是45人(含45人)以内的按标准收费,超过45人的,超出部分按八折收费.设老年团的人数为![]() .
.
(1)根据题意,用含有![]() 的式子填写下表:
的式子填写下表:
|
|
|
| |
甲宾馆收费/元 |
| 5280 | ||
乙宾馆收费/元 |
|
| 5400 |
(2)当老年人团的人数为何值时,在甲、乙两家宾馆的花费相同?如果老年人团的人数超过60人,在哪家宾馆住宿比较省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和爸爸周末步行去游泳馆游泳,爸爸先出发了一段时间后小明才出发,途中小明在离家![]() 米处的报亭休息了一段时间后继续按原来的速度前往游泳馆.爸爸、小明离家的距离
米处的报亭休息了一段时间后继续按原来的速度前往游泳馆.爸爸、小明离家的距离![]() (单位:米),
(单位:米),![]() 单位:米)与小明所走时间
单位:米)与小明所走时间![]() (单位:分钟)之间的函数关系如图所示,请结合图象信息解答下列问题:
(单位:分钟)之间的函数关系如图所示,请结合图象信息解答下列问题:

![]() 分别求出爸爸离家的距离
分别求出爸爸离家的距离![]() 和小明到达报亭前离家的距离
和小明到达报亭前离家的距离![]() 与时间
与时间![]() 之间的函数关系式;
之间的函数关系式;
![]() 求小明在报亭休息了多长时间遇到姗姗来迟的爸爸?
求小明在报亭休息了多长时间遇到姗姗来迟的爸爸?
![]() 若游泳馆离小明家
若游泳馆离小明家![]() 米,请你通过计算说明谁先到达游泳馆?
米,请你通过计算说明谁先到达游泳馆?
查看答案和解析>>
科目:初中数学 来源: 题型:
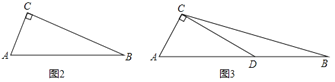
【题目】如图,平面内的两条直线l1、l2,点A、B在直线l2上,过点A、B两点分别作直线l1的垂线,垂足分别为A1、B1,我们把线段A1B1叫做线段AB在直线l2上的正投影,其长度可记作T(AB,CD)或T(AB,l2),特别地,线段AC在直线l2上的正投影就是线段A1C,请依据上述定义解决如下问题.
(1)如图1,在锐角△ABC中,AB=5,T(AC,AB)=3,则T(BC,AB)= ;
(2)如图2,在Rt△ABC中,∠ACB=90°,T(AC,AB)=4,T(BC,AB)=9,求△ABC的面积;
(3)如图3,在钝角△ABC中,∠A=60°,点D在AB边上,∠ACD=90°,T(AD,AC)=2,T(BC,AB)=6,求T(BC,CD).

查看答案和解析>>
科目:初中数学 来源: 题型:
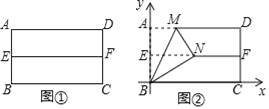
【题目】在我们学习过的数学教科书中,有一个数学活动,其具体操作过程是:
第一步:对折矩形纸片![]() ,使
,使![]() 与
与![]() 重合,得到折痕
重合,得到折痕![]() ,把纸片展开(如图①);
,把纸片展开(如图①);
第二步:再一次折叠纸片,使点![]() 落在
落在![]() 上,并使折痕经过点
上,并使折痕经过点![]() ,得到折痕
,得到折痕![]() ,同时得到线段
,同时得到线段![]() (如图②).
(如图②).
如图②所示建立平面直角坐标系,请解答以下问题:
(Ⅰ)设直线![]() 的解析式为
的解析式为![]() ,求
,求![]() 的值;
的值;
(Ⅱ)若![]() 的延长线与矩形
的延长线与矩形![]() 的边
的边![]() 交于点
交于点![]() ,设矩形的边
,设矩形的边![]() ,
,![]() ;
;
(i)若![]() ,
,![]() ,求
,求![]() 点的坐标;
点的坐标;
(ii)请直接写出![]() 、
、![]() 应该满足的条件.
应该满足的条件.
查看答案和解析>>
科目:初中数学 来源: 题型:
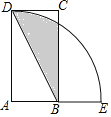
【题目】如图,四边形ABCD为矩形,以A为圆心,AD为半径的弧交AB的延长线于点E,连接BD,若AD=2AB=4,则图中阴影部分的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
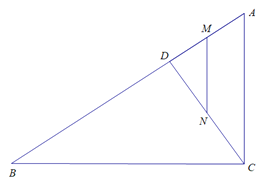
【题目】如图,在Rt⊿ABC中,∠ACB是直角, tan∠B=![]() ,BC=16 cm,点D以2cm/s的速度由点A向点B匀速运动,到达点B即停止,M、N分别是AD、CD的中点,连结MN,设点D的运动时间为t
,BC=16 cm,点D以2cm/s的速度由点A向点B匀速运动,到达点B即停止,M、N分别是AD、CD的中点,连结MN,设点D的运动时间为t
(1)求MN的长;
(2)求点D由点A到点B匀速运动过程中,线段MN所扫过的面积;
(3)若⊿DMN是等腰三角形时,求t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com