

���� ��1������������y=ax2+bx+3��x�ύ��A��C���㣬A��C���������ֱ�Ϊ��-3��0����1��0����������������ߵĽ���ʽ��
��2���ٸ����ı���OMPQ�Ǿ��Σ���֪��P����������ڵ�M�������꣬�Ӷ����������Ӧ��t��ֵ��
�ڸ�����֪������֪��������������ʱ���������������Ȼ����Ӧ��ͼ�Σ�������н���ɣ�
��� �⣺��1����������y=ax2+bx+3��x�ύ��A��C���㣬A��C���������ֱ�Ϊ��-3��0����1��0����
��$\left\{\begin{array}{l}{9a-3b+3=0}\\{a+b+3=0}\end{array}\right.$
��ã�$\left\{\begin{array}{l}{a=-1}\\{b=-2}\end{array}\right.$
�������ߵĺ�����ϵʽΪ��y=-x2-2x+3��
��2���ٵ��ı���OMPQ�Ǿ���ʱ��
��������ɵã���Q������Ϊ��-3+3t��0������M������Ϊ��0��2t������P��y=-x2-2x+3�ϣ�PQ��x�ᣬ
���P��������-3+3t��-��-3+3t��2-2��-3+3t��+3����
��-��-3+3t��2-2��-3+3t��+3=2t��
��ã�t=0��t=$\frac{10}{9}$��
�ʵ��ı���OMPQ�Ǿ���ʱ��t��ֵΪ$\frac{10}{9}$��
������QM��BC������QOM���Ե�O��B��CΪ���������������ʱ���������������
��һ�����������OQM=��OBC����QOM=��BOCʱ������ͼһ��ʾ��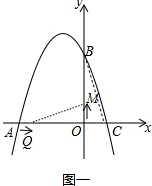
����֪�ɵã���Q������Ϊ��-3+3t��0������M������Ϊ��0��2t������C������Ϊ��1��0������B������Ϊ��0��3��
��OQ=3-3t��OM=2t��OC=1��OB=3��
�ߡ�OQM=��OBC����QOM=��BOC��
���QOM�ס�BOC��
��$\frac{OQ}{OB}=\frac{OM}{OC}$��
��$\frac{3-3t}{3}=\frac{2t}{1}$��
��ã�t=$\frac{1}{3}$��
�ڶ������������OQM=��OCB����QOM=��COB������ͼ����ʾ��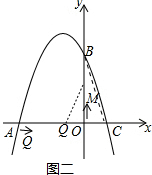
����֪�ɵã���Q������Ϊ��-3+3t��0������M������Ϊ��0��2t������C������Ϊ��1��0������B������Ϊ��0��3��
��OQ=3-3t��OM=2t��OC=1��OB=3��
�ߡ�OQM=��OCB����QOM=��COB��
���QOM�ס�BOC��
��$\frac{OQ}{OC}=\frac{OM}{OB}$��
��$\frac{3-3t}{1}=\frac{2t}{3}$��
��ã�t=$\frac{9}{11}$��
���������������OQM=��OCB����QOM=��COB������ͼ����ʾ��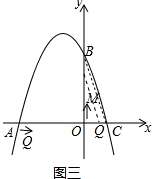
����֪�ɵã���Q������Ϊ��-3+3t��0������M������Ϊ��0��2t������C������Ϊ��1��0������B������Ϊ��0��3��
��OQ=3t-3��OM=2t��OC=1��OB=3��
�ߡ�OQM=��OCB����QOM=��COB��
���QOM�ס�BOC��
��$\frac{OQ}{OC}=\frac{OM}{OB}$��
��$\frac{3t-3}{1}=\frac{2t}{3}$��
��ã�t=$\frac{9}{7}$��
�ʴ�Ϊ��$\frac{1}{3}$��$\frac{9}{11}$��$\frac{9}{7}$��
���� ���⿼����κ����ۺ��⡢����κ����Ľ���ʽ�����ε����ʡ������ε����ơ��������۵���ѧ˼�룬����Ĺؼ�����ȷ���⣬������κ����Ľ���ʽ�����ݾ��ε����ʣ��������ν�ϵ�˼����������⣬���������ε����ƺͷ������۵���ѧ˼�������⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{15}{x+1}$-$\frac{15}{x}$=$\frac{1}{2}$ | B�� | $\frac{15}{x}-\frac{15}{x+1}=\frac{1}{2}$ | C�� | $\frac{15}{x-1}-\frac{15}{x}=\frac{1}{2}$ | D�� | $\frac{15}{x}-\frac{15}{x-1}=\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
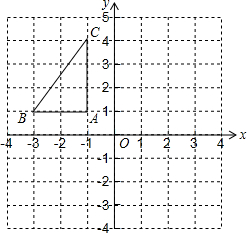 ��ͼ����ƽ��ֱ������ϵ�У���֪��ABC���������������ֱ�ΪA��-1��1����B��-3��1����C��-1��4����
��ͼ����ƽ��ֱ������ϵ�У���֪��ABC���������������ֱ�ΪA��-1��1����B��-3��1����C��-1��4�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2-$\sqrt{3}$ | B�� | $\sqrt{3}$-2 | C�� | $\sqrt{3}$+2 | D�� | -$\sqrt{3}$-2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ����������y=$\frac{{k}_{1}}{x}$��x��0����y=$\frac{{k}_{2}}{x}$��x��0����y=$\frac{{k}_{3}}{x}$��x��0����ͼ����ͼ��ʾ����k1��k2��k3�Ĵ�С��ϵ�ǣ�������
����������y=$\frac{{k}_{1}}{x}$��x��0����y=$\frac{{k}_{2}}{x}$��x��0����y=$\frac{{k}_{3}}{x}$��x��0����ͼ����ͼ��ʾ����k1��k2��k3�Ĵ�С��ϵ�ǣ�������| A�� | k1��k2��k3 | B�� | k1��k3��k2 | C�� | k3��k2��k1 | D�� | k3��k1��k2 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com