
 的圆面所覆盖.
的圆面所覆盖. 的圆纸片所覆盖.
的圆纸片所覆盖.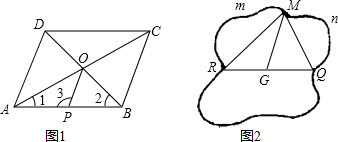
 .
. 的圆所覆盖,命题得证.
的圆所覆盖,命题得证. (MR+MQ)≤(MmR+MnQ)=
(MR+MQ)≤(MmR+MnQ)=
 长为半径的圆纸片可以覆盖住整个线圈.
长为半径的圆纸片可以覆盖住整个线圈.

 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
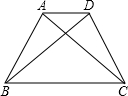 如图,已知在等腰梯形ABCD中,AD∥BC.
如图,已知在等腰梯形ABCD中,AD∥BC.| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•宝安区一模)已知矩形BEDG和矩形BNDQ中,BE=BN,DE=DN.
(2013•宝安区一模)已知矩形BEDG和矩形BNDQ中,BE=BN,DE=DN.查看答案和解析>>
科目:初中数学 来源:2010年福建省泉州五中竞赛联盟高一新生数学试卷(解析版) 题型:解答题
 的圆面所覆盖.
的圆面所覆盖. 的圆纸片所覆盖.
的圆纸片所覆盖.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com