练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】一元二次方程x2﹣8x﹣1=0配方后可变形为（ ）
    A.（x+4）2=17
    B.（x+4）2=15
    C.（x﹣4）2=17
    D.（x﹣4）2=15

    【答案】C
    【解析】解：方程变形得：x2﹣8x=1，
    配方得：x2﹣8x+16=17，即（x﹣4）2=17，
    故选C
    方程利用配方法求出解即可．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某班50名学生期末考试数学成绩（单位：分）的频率分布直方图如图所示，其中数据不在分点上，对图中提供的信息作出如下的判断：

    ②成绩在79.5～89.5分段的人数占30%；
    ③成绩在79.5分以上的学生有20人；
    ④本次考试成绩的中位数落在69.5～79.5分段内．
    其中正确的判断有（ ）
    A.4个
    B.3个
    C.2个
    D.1个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列式子：①﹣2＜0；②2x﹣3y＜0；③x=3；④x+y．其中不等式的个数有（ ）
    A.1
    B.2
    C.3
    D.4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，在 中， 是 的中点，点 在 上，点 在 上，且 .

    （1）求证： .
    （2）若 =2，求四边形 的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，平行四边形OABC的顶点A，B的坐标分别为(6，0)，(7，3)，将平行四边形OABC绕点O逆时针方向旋转得到平行四边形OA′B′C′，当点C′落在BC的延长线上时，线段OA′交BC于点E，则线段C′E的长度为________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】通过类比联想、引申拓展研究典型题目，可达到解一题知一类的目的．下面是一个案例．
    原题：如图①，点 分别在正方形 的边 上， ，连接 ，则 ，试说明理由．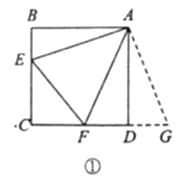

    （1）思路梳理
    因为 ，所以把 绕点 逆时针旋转90°至 ，可使 与 重合．因为 ，所以 ，点 共线．
    根据 ， 易证 ， 得 .请证明．
    （2）类比引申
    如图②，四边形 中， ， ，点 分别在边 上， .若 都不是直角，则当 与 满足等量关系时， 仍然成立，请证明．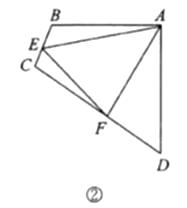

    （3）联想拓展
    如图③，在 中， ，点 均在边 上，且 .猜想 应满足的等量关系，并写出证明过程．

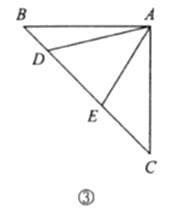
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知两个有理数a,b，如果ab<0,a+b<0,那么（ ）

    A. a>0,b<0B. a<0,b>0

    C. a,b异号D. a,b异号且负数的绝对值较大

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一组数据：﹣3，5，9，12，6的极差是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某篮球队对运动员进行3分球投篮成绩测试，每人每天投3分球10次，对甲、乙两名队员在五天中进球的个数统计结果如下：

    经过计算，甲进球的平均数为8，方差为3.2．
    （1）求乙进球的平均数和方差；
    （2）现在需要根据以上结果，从甲、乙两名队员中选出一人去参加3分球投篮大赛，你认为应该选哪名队员去？为什么？

    查看答案和解析>>

    同步练习册答案