
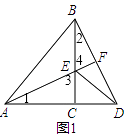
【题目】在△ABC和△DEC中,AC=BC,DC=EC,∠ACB=∠ECD=90°
(1)如图1,当点A、C、D在同一条直线上时,AC=12,EC=5
①求证:AF⊥BD ②求AF的长度;
(2)如图2,当点A、C、D不在同一条直线上时,求证:AF⊥BD; 
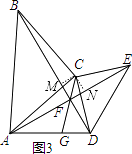
(3)如图3,在(2)的条件下,连接CF并延长CF交AD于点G,∠AFG是一个固定的值吗?若是,求出∠AFG的度数;若不是,请说明理由 
【答案】
(1)①证明:如图1,
在△ACE和△BCD中,
∵ 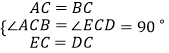 ,
,
∴△ACE≌△BCD,
∴∠1=∠2,
∵∠3=∠4,
∴∠BFE=∠ACE=90°,
∴AF⊥BD.
②∵∠ECD=90°,BC=AC=12,DC=EC=5,
∴BD= ![]() =13,
=13,
∵S△ABD= ![]() ADBC=
ADBC= ![]() BDAF,
BDAF,
即 ![]()
∴AF= ![]()
(2)证明:如图4,
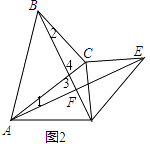
∵∠ACB=∠ECD,
∴∠ACB+∠ACD=∠ECD+∠ACD,
∴∠BCD=∠ACE,
在△ACE≌△BCD中
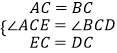
∴△ACE≌△BCD,
∴∠1=∠2,
∵∠3=∠4,
∴∠BFA=∠BCA=90°,
∴AF⊥BD
(3)∠AFG=45°,
如图3,过点C作CM⊥BD,CN⊥AE,垂足分别为M、N,
∵△ACE≌△BCD,
∴S△ACE=S△BCD,AE=BD,
∵S△ACE= ![]() AECN,
AECN,
S△BCD= ![]() BDCM,
BDCM,
∴CM=CN,
∵CM⊥BD,CN⊥AE,
∴CF平分∠BFE,
∵AF⊥BD,
∴∠BFE=90°,
∴∠EFC=45°,
∴∠AFG=45°
【解析】(1)①证明△ACE≌△BCD,得到∠1=∠2,由对顶角相等得到∠3=∠4,所以∠BFE=∠ACE=90°,即可解答;②根据勾股定理求出BD,利用△ABD的面积的两种表示方法,即可解答;(2)证明△ACE≌△BCD,得到∠1=∠2,又由∠3=∠4,得到∠BFA=∠BCA=90°,即可解答;(3)∠AFG=45°,如图3,过点C作CM⊥BD,CN⊥AE,垂足分别为M、N,由△ACE≌△BCD,得到S△ACE=S△BCD , AE=BD,证明得到CM=CN,得到CF平分∠BFE,由AF⊥BD,得到∠BFE=90°,所以∠EFC=45°,根据对顶角相等得到∠AFG=45°.


科目:初中数学 来源: 题型:
【题目】填写证明的理由.
已知:如图,AB∥CD,EF、CG分别是∠AEC、∠ECD的角平分线;求证:EF∥CG.
证明:∵AB∥CD(已知)
∴∠AEC=∠DCE ()
又∵EF平分∠AEC (已知)
∴∠1= ![]() ∠AEC ()
∠AEC ()
同理∠2= ![]() ∠DCE,∴∠1=∠2
∠DCE,∴∠1=∠2
∴EF∥CG ()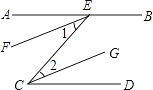
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(7分)小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).

(1)请根据题中已有的信息补全频数分布表和频数分布直方图;

(2)如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户?
(3)从月均用水量在2≤x<3,8≤x<9这两个范围内的样本家庭中任意抽取2个,求抽取出的2个家庭来自不同范围的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“综合与实践”学习活动准备制作一组三角形,记这些三角形的三边分别为a,b,c,并且这些三角形三边的长度为大于1且小于5的整数个单位长度.
(1)用记号(a,b,c)(a≤b≤c)表示一个满足条件的三角形,如(2,3,3)表示边长分别为2,3,3个单位长度的一个三角形.请列举出所有满足条件的三角形.
(2)用直尺和圆规作出三边满足a<b<c的三角形(用给定的单位长度,不写作法,保留作图痕迹). ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下列一组数: ![]() ,
, ![]() .
.
(1)将这组数分类填入相应的大括号内. 1分数集合:{…};
2无理数集合:{…};
3非负数集合:{…}.
(2)在数轴上标出这组数对应的点的大致位置,并用“<”把它们连接起来.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com