【题目】某电脑批发商第一天运进50台电脑，第二天运进－32台电脑，第三天运进40台电脑，第四天运进－29台电脑，如果运进记作正的，那么四天共运进电脑多少台？
科目：初中数学 来源： 题型：
【题目】（操作发现）
在计算器上输入一个正数，不断地按“
”键求算术平方根，运算结果越来越接近1或都等于1．
【提出问题】
输入一个实数，不断地进行“乘以常数k，再加上常数b”的运算，有什么规律？
【分析问题】
我们可用框图表示这种运算过程（如图a）．
也可用图象描述：如图1，在x轴上表示出x1，先在直线y=kx+b上确定点（x1，y1），再在直线y=x上确定纵坐标为y1的点（x2，y1），然后再x轴上确定对应的数x2，…，以此类推．
【解决问题】
研究输入实数x1时，随着运算次数n的不断增加，运算结果x，怎样变化．
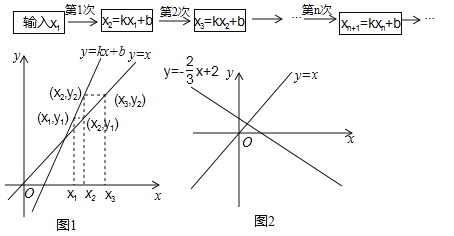
（1）若k=2，b=﹣4，得到什么结论？可以输入特殊的数如3，4，5进行观察研究；
（2）若k＞1，又得到什么结论？请说明理由；
（3）①若
，b=2，已在x轴上表示出x1（如图2所示），请在x轴上表示x2，x3，x4，并写出研究结论；
②若输入实数x1时，运算结果xn互不相等，且越来越接近常数m，直接写出k的取值范围及m的值（用含k，b的代数式表示）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读：我们约定，在平面直角坐标系中，经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线，叫该点的“特征线”．例如，点M（1，3）的特征线有：x=1，y=3，y=x+2，y=﹣x+4．
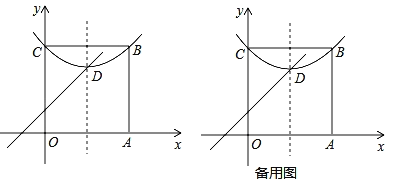
问题与探究：如图，在平面直角坐标系中有正方形OABC，点B在第一象限，A、C分别在x轴和y轴上，抛物线
经过B、C两点，顶点D在正方形内部．
（1）直接写出点D（m，n）所有的特征线；
（2）若点D有一条特征线是y=x+1，求此抛物线的解析式；
（3）点P是AB边上除点A外的任意一点，连接OP，将△OAP沿着OP折叠，点A落在点A′的位置，当点A′在平行于坐标轴的D点的特征线上时，满足（2）中条件的抛物线向下平移多少距离，其顶点落在OP上？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】观察下面的变形规律：
=1﹣ 
； 
= ﹣ 
； 
= ﹣ 
；…解答下面的问题：
（1）若n为正整数，请你猜想 
=；
（2）求和： + + ．（注：只能用上述结论做才能给分）；
（3）用上述相似的方法求和： 
+ 
+ 
+…+ 
．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】二次函数y=x2+2x﹣3的开口方向、顶点坐标分别是（ ）
A.开口向上，顶点坐标为（﹣1，﹣4）
B.开口向下，顶点坐标为（1，4）
C.开口向上，顶点坐标为（1，4）
D.开口向下，顶点坐标为（﹣1，﹣4）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们知道，任意一个正整数n都可以进行这样的分解：n=p×q（p，q是正整数，且p≤q），在n的所有这种分解中，如果p，q两因数之差的绝对值最小，我们就称p×q是n的最佳分解．并规定：F（n）=
．例如12可以分解成1×12，2×6或3×4，因为12﹣1＞6﹣2＞4﹣3，所有3×4是12的最佳分解，所以F（12）=
．
（1）如果一个正整数a是另外一个正整数b的平方，我们称正整数a是完全平方数．求证：对任意一个完全平方数m，总有F（m）=1；
（2）如果一个两位正整数t，t=10x+y（1≤x≤y≤9，x，y为自然数），交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18，那么我们称这个数t为“吉祥数”，求所有“吉祥数”中F（t）的最大值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列说法中：（1）垂直于弦的直径平分这条弦并且平分这条弦所对的两条弧；（2）半圆是弧；（3）长度相等的弧是等弧；（4）平分弦的直径垂直于这条弦；正确的个数有（ ）
A.0个B.1个C.2个D.3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
