
【题目】一张如图1的长方形铁皮,四个角都剪去边长为30厘米的正方形,再四周折起,做成一个有底无盖的铁盒如图2,铁盒底面长方形的长是4a(cm),宽是3a(cm),这个无盖铁盒各个面的面积之和称为铁盒的全面积.
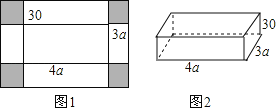
(1)请用a的代数式表示图1中原长方形铁皮的面积;
(2)若要在铁盒的各个外表面漆上某种油漆,每元钱可漆的面积为![]() (cm2),则油漆这个铁盒需要多少钱(用a的代数式表示)?
(cm2),则油漆这个铁盒需要多少钱(用a的代数式表示)?
(3)铁盒的底面积是全面积的几分之几(用a的代数式表示)?若铁盒的底面积是全面积的![]() ,求a的值;
,求a的值;
(4)是否存在一个正整数a,使得铁盒的全面积是底面积的正整数倍?若存在,请求出这个a,若不存在,请说明理由.
【答案】(1)12a2+420a+3600;
(2)600a+21000(元);
(3)a=105;
(4)存在铁盒的全面积是底面积的正整数倍,这时a=35或7或5或1.
【解析】
试题分析:(1)根据图形表示出原长方形铁皮的面积即可;
(2)根据原长方形铁皮的面积剪去四个小正方形的面积,求出铁盒的表面积,乘以单价即可得到结果;
(3)用铁盒的底面积除以全面积即可得出底面积是全面积的几分之几,再根据铁盒的底面积是全面积的![]() ,求出a的值即可;
,求出a的值即可;
(4)假设存在,列出铁盒的全面积和底面积的公式,求整数倍数即可.
解:(1)原铁皮的面积是(4a+60)(3a+60)=12a2+420a+3600;
(2)油漆这个铁盒的表面积是:12a2+2×30×4a+2×30×3a=12a2+420a,
则油漆这个铁盒需要的钱数是:(12a2+420a)÷![]() =(12a2+420a)×
=(12a2+420a)×![]() =600a+21000(元);
=600a+21000(元);
(3)铁盒的底面积是全面积的![]() =
=![]() ;
;
根据题意得:![]() =
=![]() ,
,
解得a=105;
(4)铁盒的全面积是4a×3a+4a×30×2+3a×30×2=12a2+420a,
底面积是12a2,
假设存在正整数n,使12a2+420a=n(12a2)
则(n﹣1)a=35,
则a=35,n=2或a=7,n=6或a=5,n=8或a=1,n=36
所以存在铁盒的全面积是底面积的正整数倍,这时a=35或7或5或1.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
【题目】如图,二次函数的图象与x轴交于A(﹣3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.

(1)求二次函数的解析式;
(2)根据图象直接写出使一次函数值大于二次函数值的x的取值范围;
(3)若直线与y轴的交点为E,连结AD、AE,求△ADE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简,再求值:
(1)3x2﹣[5x﹣(6x﹣4)﹣2x2],其中x=3
(2)(8mn﹣3m2)﹣5mn﹣2(3mn﹣2m2),其中m=﹣1,n=2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某地区45000名九年级学生的睡眠情况,运用所学统计知识解决上述问题所要经历的几个主要步骤:①抽样调查;②设计调查问卷;③用样本估计总体;④整理数据;⑤分析数据,按操作的先后进行排序为____.(只写序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
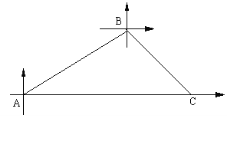
【题目】甲、乙两条轮船同时从港口A出发,甲轮船以每小时30海里的速度沿着北偏东60°的方向航行,乙轮船以每小时15海里的速度沿着正东方向行进,1小时后,甲船接到命令要与乙船会和,于是甲船改变了行进的速度,沿着东南方向航行,结果在小岛C处与乙船相遇.假设乙船的速度和航向保持不变,求港口A与小岛C之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,直线x=﹣1是对称轴,有下列判断:①b﹣2a=0;②4a﹣2b+c<0;③a﹣b+c=﹣9a;④若(﹣3,y1),(![]() ,y2)是抛物线上两点,则y1>y2,其中正确的个数是( )
,y2)是抛物线上两点,则y1>y2,其中正确的个数是( )
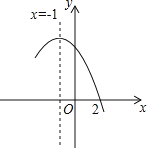
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com