Question

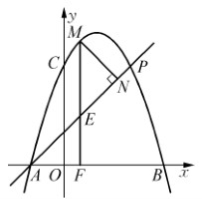
如图所示，已知二次函数经过、、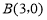C三点，点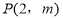是抛物线与直线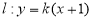的一个交点．

（1）求二次函数关系式和点C的坐标；

（2）对于动点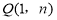，求的最大值；

（3）若动点M在直线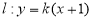上方的抛物线运动，过点M做x轴的垂线交x轴于点F，如果直线AP把线段MF分成1:2的两部分，求点M的坐标。

 

 

Answer 1

（1）函数关系式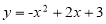：; C点坐标为（0,3）

（2）

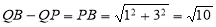
（3）M的坐标为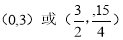

【解析】

试题分析：(1)本题考查的是二次函数的性质以及待定系数法求二次函数解析式的相关知识，我们要注意根据已知条件选择合适的关系式的设法，本题利用一般式，由于已知常数项，再把两点坐标代入关系式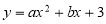，得到关于a、b的二元一次方程组，解方程组求出a、b的值，关系式便可得出.C点坐标为（0,3）(2)把函数关系式写成顶点式的形式后，可以知道动点在二次函数的对称轴上，只有当Q、P、B三点共线时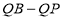，的值最大.(3)由于点M、E都在x轴上方，MF∥y轴，ME=yM-yE EF=yE MF=yM 线段MF分成1:2的两部分注意有两种情况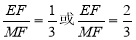，见题解.

试题解析：解（1）把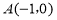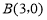两点坐标代入关系式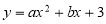得a=-1,b=2

∴函数关系式为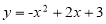.由函数关系式得C点坐标为（0,3）.

（2）如图：因为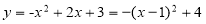，所以动点Q（1，n)在二次函数的对称轴上。 所以当点Q、P、B三点共线时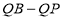，的值最大，最大值为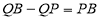

把x=2代入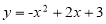，得y=3

即点P的坐标为（2,3）,又因为B（3,0）

所以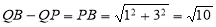

（3）因为点P坐标为（2，3）代入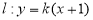得k=1

所以直线l的关系式为：y=x+1

因为AP把线段MF分成1:2的两部分，

则根据题意，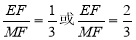

设点M的横坐标为x，那么

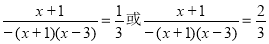
解得x=0或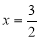

代入y=x+1得：y=3或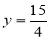

所以点M的坐标为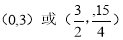

考点：1、待定系数法求二次函数解析式；2、二次函数的图象；3、平面直角坐标系中线段的长度的表示方法；4、三点共线时，两线段之差是最大值.