
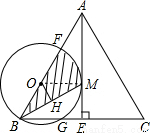
如图△ABC中,AB=AC,AE⊥BC,E为垂足,F为AB上一点.以BF为直径的圆与AE相切于M点,交BC于G点.
(1)求证:BM平分∠ABC;
(2)当BC=4,cosC= 时,
时,
①求⊙O的半径;
②求图中阴影部分的面积.(结果保留π与根号)

(1)证明见解析;(2)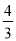 ;
;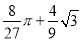 .
.
【解析】
试题分析:(1)连OM,根据切线的性质得OM⊥AE,而AE⊥BC,则OM∥BC,根据平行线的性质得∠OMB=∠MBC,而∠OBM=∠OMB,所以∠OBM=∠MBE;
(2)①设⊙O的半径为R,根据等腰三角形的性质得BE=CE=2,由cos∠C=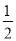 得到∠C=60°,则可判断△ABC为等边三角形,所以AB=AC=BC=4,则∠OAM=30°,根据含30度的直角三角形三边的关系得到AO=2R,则2R+R=4,解得R=
得到∠C=60°,则可判断△ABC为等边三角形,所以AB=AC=BC=4,则∠OAM=30°,根据含30度的直角三角形三边的关系得到AO=2R,则2R+R=4,解得R=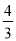 ;
;
②过O作OH⊥BM,H为垂足,根据垂径定理得BH=MH,易得∠AOM=60°,∠ABH=30°,根据含30度的直角三角形三边的关系可得OH=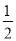 OB=
OB=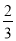 ,BH=
,BH=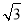 OH=
OH=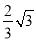 ,所以BM=
,所以BM=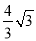 ,然后根据扇形面积公式和三角形面积公式和S阴=S扇形FOM+S△OBM进行计算.
,然后根据扇形面积公式和三角形面积公式和S阴=S扇形FOM+S△OBM进行计算.
(1)证明:连OM,如图,
∵⊙O与AE相切于M,
∴OM⊥AE,
∵AE⊥BC,
∴OM∥BC,
∴∠OMB=∠MBC,
∵OB=OM,
∴∠OBM=∠OMB,
∴∠OBM=∠MBE,
∴BM平分∠ABC;
(2)【解析】
①设⊙O的半径为R,
∵AB=AC,BC=4,AE⊥BC,
∴BE=CE=2,
在Rt△ACE中,cos∠C=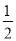 ,
,
∴∠C=60°
∴△ABC为等边三角形,
∴AB=AC=BC=4,
∴∠OAM=30°,
∴AO=2R,
而AB=OA+BO,
∴2R+R=4,
∴R=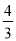 ,
,
即⊙O的半径为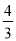 ;
;
②过O作OH⊥BM,H为垂足,如图,
∵OH⊥BM,
∴BH=MH,
∵OM∥BE,
∴∠AOM=60°,
∴∠ABH=30°,
∴OH=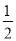 OB=
OB=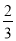 ,BH=
,BH=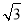 OH=
OH=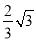 ,
,
∴BM=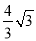 ,
,
∴S△OBM=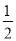 OH•BM=
OH•BM=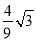 ,
,
∴S扇形FOM=
∴S阴=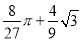 .
.
考点:1.切线的性质;2.扇形面积的计算.


科目:初中数学 来源:2013-2014学年江苏省淮安市洪泽县九年级中考二模数学试卷(解析版) 题型:解答题
如图所示,已知二次函数 经过
经过 、
、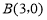 、C三点,点
、C三点,点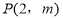 是抛物线与直线
是抛物线与直线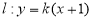 的一个交点.
的一个交点.
(1)求二次函数关系式和点C的坐标;
(2)对于动点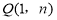 ,求
,求 的最大值;
的最大值;
(3)若动点M在直线 上方的抛物线运动,过点M做x轴的垂线交x轴于点F,如果直线AP把线段MF分成1:2的两部分,求点M的坐标。
上方的抛物线运动,过点M做x轴的垂线交x轴于点F,如果直线AP把线段MF分成1:2的两部分,求点M的坐标。
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省淮安市洪泽县九年级中考二模数学试卷(解析版) 题型:选择题
为响应“节约用水”的号召,小李随机调查了班级35名同学中5名同学家庭一年的平均用水量(单位:吨),记录如下:8,9,8,7,10,这组数据的平均数和中位数分别是( )
A.8,8 B.8.4,8 C.8.4,8.4 D.8,8.4
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省泰州市姜堰区中考适应性考试数学试卷(解析版) 题型:解答题
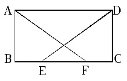
如图,在□ABCD中,E、F为BC上的两点,且BE=CF,AF=DE.
求证:(1)△ABF≌△DCE;
(2)四边形ABCD是矩形.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省泰州市姜堰区中考适应性考试数学试卷(解析版) 题型:填空题
某商场销售额3月份为16万元,5月份为25万元,则该商场这两个月销售额的平均增长率是 .
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省江阴市要塞片九年级下学期期中考试数学试卷(解析版) 题型:解答题
如图,“五一”节,小明和同学一起到游乐场游玩,游乐场的大型摩天轮的半径为20米,旋转1周需要24分钟(匀速)。小明乘坐最底部的车厢按逆时针方向旋转(离地面约1米)开始1周的观光。
(1)4分钟后小明离地面的高度是多少?
(2)摩天轮启动多长时间后,小明离地面的高度到达11米?
(3)在旋转一周的过程中,小明将有多长时间连续保持在离地面31米以上的空中?

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省江阴市九年级下学期期中考试数学试卷(解析版) 题型:选择题
如图1,在平面直角坐标系中,将□ABCD放置在第一象限,且AB∥x轴.直线
y=-x从原点出发沿x轴正方向平移,在平移过程中直线被平行四边形截得的线段长度l与直线在x轴上平移的距离m的函数图象如图2所示,那么ABCD面积为( )
A.4 B.4 C.8 D.8
C.8 D.8

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com