
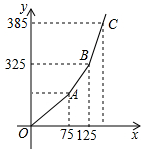
 为增强公民的节约意识,合理利用天然气资源,某市自1月1日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如表所示:
为增强公民的节约意识,合理利用天然气资源,某市自1月1日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如表所示:| 每月用气量 | 单价(元/m3) |
| 不超出75m3的部分 | 2.5 |
| 超出75m3不超过125m3的部分 | a |
| 超出125m3的部分 | a+0.25 |
分析 (1)根据单价×数量=总价就可以求出3月份应该缴纳的费用;
(2)结合统计表的数据)根据单价×数量=总价的关系建立方程就可以求出a值,再从0≤x≤75,75<x≤125和x>125运用待定系数法分别表示出y与x的函数关系式即可.
解答 解:(1)由题意,得
60×2.5=150(元);
(2)由题意,得
a=(325-75×2.5)÷(125-75),
a=2.75,
∴a+0.25=3,
设OA的解析式为y1=k1x,则有
2.5×75=75k1,
∴k1=2.5,
∴线段OA的解析式为y1=2.5x(0≤x≤75);
设线段AB的解析式为y2=k2x+b,由图象,得
$\left\{\begin{array}{l}{187.5=72{k}_{2}+b}\\{325=125{k}_{2}+b}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{k}_{2}=2.75}\\{b=-18.75}\end{array}\right.$,
∴线段AB的解析式为:y2=2.75x-18.75(75<x≤125);
(385-325)÷3=20,故C(145,385),设射线BC的解析式为y3=k3x+b1,由图象,得
$\left\{\begin{array}{l}{325=125{k}_{3}+{b}_{1}}\\{385=14{5k}_{3}+{b}_{1}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{3}=3}\\{{b}_{1}=-50}\end{array}\right.$,
∴射线BC的解析式为y3=3x-50(x>125).
点评 本题是一道一次函数的综合试题,考查了单价×数量=总价的运用,待定系数法求一次函数的解析式的运用,分段函数的运用,分类讨论思想在解实际问题的运用,解答时求出函数的解析式是关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
| -30 | +82 | -19 | +102 | -96 | +34 | -28 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 观察函数y1=k1x+b1和y2=k2x+b2的图象,当x=1,两个函数值的大小为( )
观察函数y1=k1x+b1和y2=k2x+b2的图象,当x=1,两个函数值的大小为( )| A. | y1=y2 | B. | y1≥y2 | C. | y1>y2 | D. | y1<y2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com