

分析 [探究一]根据等腰直角三角形“三合一”的性质推知BE是直角三角形ABC斜边AC上的中线,然后由直角三角形斜边上的中线是斜边的一半即可求得BE=AE=5$\sqrt{2}$;
[探究二](1)①连接BE,根据已知条件得到E是AC的中点,根据等腰直角三角形的性质可以证明DE=CE,∠PBE=∠C.根据等角的余角相等可以证明∠BEP=∠CEQ.即可得到全等三角形,从而证明结论;
②利用①中全等三角形的性质知S△BEP=S△CEQ,然后根据图形知S四边形EPBQ=S△ABC-S△APE-S△CEQ=S△ABC-S△APE-S△BEP=S△ABC-S△ABE=$\frac{1}{2}$S△ABC;
(2)作EM⊥AB,EN⊥BC于M、N,根据两个角对应相等证明△MEP∽△NWQ,发现EP:EQ=EM:EN,再根据等腰直角三角形的性质得到EM:EN=AE:CE;
(3)根据(2)中求解的过程,可以直接写出结果.
解答 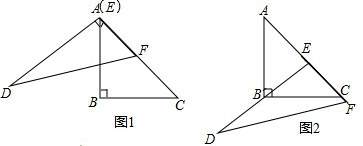 解:[探究一]如图2,在△ABC中,∠ABC=90°,AB=BC=10,
解:[探究一]如图2,在△ABC中,∠ABC=90°,AB=BC=10,
∴AC=10$\sqrt{2}$(勾股定理);
又∵BE⊥AC,
∴BE=AE=$\frac{1}{2}$AC=5$\sqrt{2}$(直角三角形斜边上的中线是斜边的一半);
即三角板DEF沿A→C方向平移的距离为5$\sqrt{2}$;
故答案是:5$\sqrt{2}$;
[探究二]
(1)①如图3,连接BE,根据E是AC的中点和等腰直角三角形的性质,得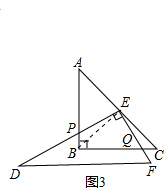
∠PBE=∠C,BE=CE,
又∠BEP=∠CEQ,
则△BEP≌△CEQ,得EP=EQ;
故答案是:√;
②由①知,△BEP≌△CEQ,
∴S△BEP=S△CEQ,
∴S四边形EPBQ=S△ABC-S△APE-S△CEQ=S△ABC-S△APE-S△BEP=S△ABC-S△ABE;
又∵BE是直角三角形ABC斜边AC上的中垂线,
∴S△ABE=$\frac{1}{2}$S△ABC,
∴S四边形EPBQ=$\frac{1}{2}$S△ABC;
故答案是:√;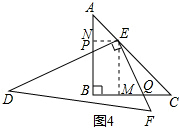
(2)EQ=2EP.理由如下:
如图4,过E作EM⊥BC于M,过E作EN⊥AB于N,
则EM=$\frac{\sqrt{2}}{2}$EC,EN=$\frac{\sqrt{2}}{2}$AE,
∵$\frac{CE}{EA}$=2,
∴$\frac{EM}{EN}$=2.
∵∠QEM+∠MEP=∠PEN+∠MEP=90°,
∴∠QEM=∠PEN,
又∠EMQ=∠ENP,
∴△EMQ∽△ENP,
∴$\frac{EQ}{EP}$,即:EQ=2EP;
(3)由(1)知,当$\frac{CE}{EA}$=1时,EP=EQ;
由(2)知,当$\frac{CE}{EA}$=2时,EP=2EQ;
∴当$\frac{CE}{EA}$=m时,EP=mEQ;
故答案是:EQ=mEP.
点评 本题考查的是四边形综合题.熟练运用等腰直角三角形的性质和相似三角形的判定和性质进行求解.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
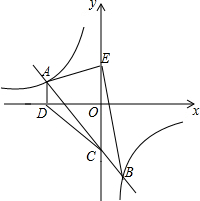 如图,一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于第二象限的点A(m,1),且与y轴交于点C.过点A作x轴的垂线,垂足为点D,连接CD,已知△ADC的面积为$\frac{3}{2}$,且tan∠ACO=1.
如图,一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于第二象限的点A(m,1),且与y轴交于点C.过点A作x轴的垂线,垂足为点D,连接CD,已知△ADC的面积为$\frac{3}{2}$,且tan∠ACO=1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 月份 | 用水量(m3) | 收费(元) |
| 9 | 5 | 7.5 |
| 10 | 9 | 27 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com