练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
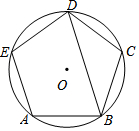
    2．如图，正五边形ABCDE内接于⊙O，则∠ABD的度数为（　　）
    A．36°B．72°C．108°D．144°

    分析 根据多边形内角和定理、正五边形的性质求出∠ABC、CD=CB，根据等腰三角形的性质求出∠CBD，计算即可．

    解答 解：∵五边形ABCDE为正五边形，
    ∴∠ABC=∠C=$\frac{（5-2）×180°}{5}$=108°，
    ∵CD=CB，
    ∴∠CBD=$\frac{180°-108°}{2}$=36°，
    ∴∠ABD=∠ABC-∠CBD=72°，
    故选B．

    点评 本题考查的是正多边形和圆、多边形的内角和定理，掌握正多边形和圆的关系、多边形内角和等于（n-2）×180°是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    12．如图放置的△OAB1，△B1A1B2，△B2A2B3，…都是边长为1的等边三角形，点A在x轴上，点O，B1，B2，B3，…都在直线l上，则点A2的坐标是（2，$\sqrt{3}$），点A2017的坐标是（$\frac{2019}{2}$，$\frac{2017\sqrt{3}}{2}$）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．已知$\root{3}{x}$=4，且（y3-2x+3）2+$\sqrt{z-3}$=0，求$\root{3}{x+{y}^{3}+{z}^{3}}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．矩形ABCD的边AB=3 cm，AD=4 cm，以A为圆心，4 cm为半径作⊙A，则点C与⊙A的位置关系为（　　）
    A．点C在⊙A内B．点C不一定在⊙A外C．点C在⊙A上D．点C在⊙A外

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．如图，已知∠1=∠2，则不一定能使△ABD≌△ACD的条件是（　　）
    A．BD=CDB．AB=ACC．∠B=∠CD．∠BDA=∠CDA

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

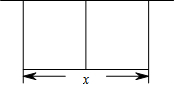    7．某农场拟建两间矩形种牛饲养室，饲养室的一面靠现有墙（墙长＞50m），中间用一道墙隔开（如图），己知计划中的建筑材料可建围墙的总长为50m，设两饲养室合计长x（m），总占地面积为y（m2）
    （1）求y关于x的函数表达式和自变量的取值范围；
    （2）若要使两间饲养室占地总面积达到200m2，则各道墙的长度为多少？占地总面积有可能达到210m2吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．若单项式x2ym-n与单项式-$\frac{1}{2}{x^{2m+n}}{y^3}$是同类项，那么这两个多项式的和是（　　）
    A．$\frac{1}{2}{x^4}{y^6}$B．$\frac{1}{2}{x^2}{y^3}$C．$\frac{3}{2}{x^2}{y^3}$D．$-\frac{1}{2}{x^2}{y^3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．化简：
    （1）（2x-1）（2x+1）+（4x+3）（x-6）
    （2）（2a+3b）2-4a（a+3b）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．计算（$\frac{1}{2017}$）-1+2$\sqrt{\frac{1}{4}}$-（π-$\sqrt{9}$）0-$\sqrt{3}$cot30°．

    查看答案和解析>>

    同步练习册答案