
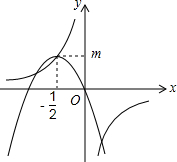
 如图,双曲线y=$\frac{k}{x}$经过抛物线y=ax2+bx的顶点(-$\frac{1}{2}$,m)(m>0),则有( )
如图,双曲线y=$\frac{k}{x}$经过抛物线y=ax2+bx的顶点(-$\frac{1}{2}$,m)(m>0),则有( )| A. | a=b+2k | B. | a=b-2k | C. | k<b<0 | D. | a<k<0 |
分析 根据抛物线的开口方向和反比例函数所处的象限判断a<0,k<0,根据对称轴x=-$\frac{b}{2a}$=-$\frac{1}{2}$得出a=b,由双曲线y=$\frac{k}{x}$经过抛物线y=ax2+bx的顶点(-$\frac{1}{2}$,m)(m>0),对称k=-$\frac{1}{2}$m,m=$\frac{1}{4}$a-$\frac{1}{2}$b,进而对称8k=a=b,即可得出a<k<0.
解答 解:∵抛物线y=ax2+bx的顶点(-$\frac{1}{2}$,m),
∴对称轴x=-$\frac{b}{2a}$=-$\frac{1}{2}$,
∴a=b<0,
∵双曲线y=$\frac{k}{x}$经过抛物线y=ax2+bx的顶点(-$\frac{1}{2}$,m)(m>0),
∴k=-$\frac{1}{2}$m,m=$\frac{1}{4}$a-$\frac{1}{2}$b,
∴m=-2k,m=-$\frac{1}{4}$a=-$\frac{1}{4}$b,
∴-2k=-$\frac{1}{4}$a=-$\frac{1}{4}$b,
∴8k=a=b,
∵a<0,
∴a<k<0,
故选D.
点评 本题考查了二次函数图象与系数的关系,利用抛物线的顶点坐标和二次函数图象上点的坐标特征是解题的关键.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:解答题
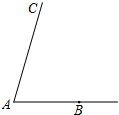 如图,已知∠CAB,用直尺和圆规作∠ABD,使∠ABD=$\frac{1}{2}$∠A,射线BD与射线AC相交于点D.(不写画法,保留作图痕迹)
如图,已知∠CAB,用直尺和圆规作∠ABD,使∠ABD=$\frac{1}{2}$∠A,射线BD与射线AC相交于点D.(不写画法,保留作图痕迹)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
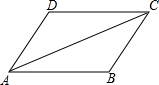 用2根同样长的木条AB,CD和另外两根同样长的木条AD,BC拼成一个四边形ABCD,
用2根同样长的木条AB,CD和另外两根同样长的木条AD,BC拼成一个四边形ABCD,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
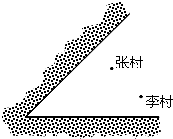 近年来,江苏省实施“村村通”工程和农村医疗卫生改革,宜兴市计划在某镇的张村、李村之间建一座定点医疗站P,张、李两村坐落在两相交公路内(如图所示),医疗站必须满足下列条件:①使其到两公路的距离相等;②到张、李两村的距离也相等.请你利用尺规作图确定P点的位置.(不写作法,保留作图痕迹)
近年来,江苏省实施“村村通”工程和农村医疗卫生改革,宜兴市计划在某镇的张村、李村之间建一座定点医疗站P,张、李两村坐落在两相交公路内(如图所示),医疗站必须满足下列条件:①使其到两公路的距离相等;②到张、李两村的距离也相等.请你利用尺规作图确定P点的位置.(不写作法,保留作图痕迹)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,是正方体包装盒的平面展开图,如果在其中的三个正方形A、B、C内分别填上适当的数,使得将这个平面展开图折成正方体后,相对面上的两数字互为相反数,则填在A、B、C内的三个数字依次为( )
如图,是正方体包装盒的平面展开图,如果在其中的三个正方形A、B、C内分别填上适当的数,使得将这个平面展开图折成正方体后,相对面上的两数字互为相反数,则填在A、B、C内的三个数字依次为( )| A. | 0,1,-2 | B. | 1,0,-2 | C. | -2,0,1 | D. | 0,-2,1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
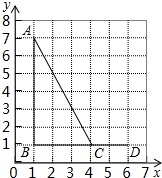 如图,点A、B、C、D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C、D、E为顶点的三角形与△ABC相似,则下列坐标不可能是点E的坐标的是( )
如图,点A、B、C、D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C、D、E为顶点的三角形与△ABC相似,则下列坐标不可能是点E的坐标的是( )| A. | (4,0) | B. | (6,0) | C. | (6,4) | D. | (4,5) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
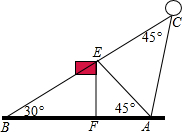 如图,某校20周年校庆时,需要在草场上利用气球悬挂宣传条幅,EF为旗杆,气球从A处起飞,几分钟后便飞达C处,此时,在AF延长线上的点B处测得气球和旗杆EF的顶点E在同一直线上.
如图,某校20周年校庆时,需要在草场上利用气球悬挂宣传条幅,EF为旗杆,气球从A处起飞,几分钟后便飞达C处,此时,在AF延长线上的点B处测得气球和旗杆EF的顶点E在同一直线上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两点确定一条直线 | B. | 两点之间线段最短 | ||
| C. | 过一点有无数条直线 | D. | 线段是直线的一部分 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com