
【题目】已知锐角![]() 如图,
如图,

(1)在射线![]() 上取一点
上取一点![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 长为半径作弧
长为半径作弧![]() ,交射线
,交射线![]() 于点
于点![]() ,连接
,连接![]() ;
;
(2)以点![]() 为圆心,
为圆心,![]() 长为半径作弧,交弧
长为半径作弧,交弧![]() 于点
于点![]() ;
;
(3)连接![]() ,
,![]() .作射线
.作射线![]() .
.
根据以上作图过程及所作图形,下列结论中错误的是( )
A.![]() B.若
B.若![]() ,则
,则![]()
C.![]() 垂直平分
垂直平分![]() D.
D.![]()
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(a,0),B(0,a),等腰直角三角形ODC的斜边经过点B,OE⊥AC,交AC于E,若OE=2,则△BOD与△AOE的面积之差为( )

A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了发展乡村旅游,某村准备在河道上修一座与河道垂直的桥,如图(1)所示,直线l,m代表河流的两岸河道,且l∥m,点A是某村自助农场的所在地,点B是某村游乐场所在地.

问题1:造桥选址桥准备选在到A,B两地的距离之和刚好为最小的点C处,即在直线l上找一点C,使AC+BC的值为最小.请利用你所学的知识在图(1)中作出点C的位置,并简单说明你所设计方案的原理;
问题2:测量河宽:在测量河道的宽度时施工队在河道南侧的开阔地用以下方法(如图2所示):①作CD⊥l,与河对岸的直线m相交于D;②在直线m上取E,F两点,使得DE=EF=10米;③过点F作m的垂线FG,使得点G与C,E两点在同一直线上;④测量FG的长度为20米.请你确定河道的宽度,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一条船上午![]() 点在
点在![]() 处望见西南方向有一座灯塔
处望见西南方向有一座灯塔![]() (如图),此时测得船和灯塔相距
(如图),此时测得船和灯塔相距![]() 海里,船以每小时
海里,船以每小时![]() 海里的速度向南偏西
海里的速度向南偏西![]() 的方向航行到
的方向航行到![]() 处,这时望见灯塔在船的正北方向.(参考数据:
处,这时望见灯塔在船的正北方向.(参考数据:![]() ,
,![]() ).
).

![]() 求几点钟船到达
求几点钟船到达![]() 处;
处;
![]() 求船到达
求船到达![]() 处时与灯塔
处时与灯塔![]() 之间的距离.
之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
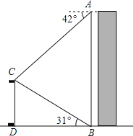
【题目】如图,某校数学兴趣小组在楼![]() 的顶部
的顶部![]() 处测得该楼正前方旗杆
处测得该楼正前方旗杆![]() 的顶端
的顶端![]() 的俯角为
的俯角为![]() ,在楼
,在楼![]() 的底部
的底部![]() 处测得旗杆
处测得旗杆![]() 的顶端
的顶端![]() 的仰角为
的仰角为![]() ,已知旗杆
,已知旗杆![]() 的高度为
的高度为![]() ,根据测得的数据,计算楼
,根据测得的数据,计算楼![]() 的高度(结果保留整数).
的高度(结果保留整数).
参考数据:![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a使关于x的不等式组 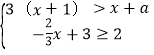 有两个整数解,且使关于x的方程
有两个整数解,且使关于x的方程![]() 有负数解,则符合题意的整数a的个数有 ( )
有负数解,则符合题意的整数a的个数有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (x>0,m≠0)的图象交于点C,与x轴、y轴分别交于点D、B,已知OB=3,点C的横坐标为4,cos∠0BD=
(x>0,m≠0)的图象交于点C,与x轴、y轴分别交于点D、B,已知OB=3,点C的横坐标为4,cos∠0BD=![]()
(1)求一次函数及反比例函数的表达式;
(2)将一次函数图象向下平移,使其经过原点O,与反比例函数图象在第四象限内的交点为A,连接AC,求四边形OACB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的直角坐标系中,解答下列问题.
(1)分别写出A、B两点的坐标:A ,B .
(2)△ABC的面积= ;点B到AC的距离= .
(3)画出△ABC关于x轴对称的△A1B1C1.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知半圆![]() 的直径
的直径![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,半圆
,半圆![]() 以
以![]() 的速度从左向右运动,在运动过程中,点
的速度从左向右运动,在运动过程中,点![]() 、
、![]() 始终在直线
始终在直线![]() 上.设运动时间为
上.设运动时间为![]() ,当
,当![]() 时,半圆
时,半圆![]() 在
在![]() 的左侧,
的左侧,![]() .
.
![]() 当
当![]() 为何值时,
为何值时,![]() 的一边所在直线与半圆
的一边所在直线与半圆![]() 所在的圆相切?
所在的圆相切?
![]() 当
当![]() 的一边所在直线与半圆
的一边所在直线与半圆![]() 所在的圆相切时,如果半圆
所在的圆相切时,如果半圆![]() 与直线
与直线![]() 围成的区域与
围成的区域与![]() 三边围成的区域有重叠部分,求重叠部分的面积.
三边围成的区域有重叠部分,求重叠部分的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com