
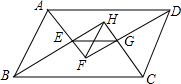
 如图,在?ABCD中,AF、BH、CH、DF分别是∠DAB、∠ABC、∠BCD与∠CDA的平分线,AF与BH交于点E,CH与DF交于点G.求证:EG=FH.
如图,在?ABCD中,AF、BH、CH、DF分别是∠DAB、∠ABC、∠BCD与∠CDA的平分线,AF与BH交于点E,CH与DF交于点G.求证:EG=FH.  王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:选择题
| A. | y1<y2 | B. | y1=y2 | C. | y1>y2 | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,PA切⊙于点A,OP交⊙O于点B,且点B为OP的中点,弦AC∥OP.若OP=2,则图中阴影部分的面积为( )
如图,PA切⊙于点A,OP交⊙O于点B,且点B为OP的中点,弦AC∥OP.若OP=2,则图中阴影部分的面积为( )| A. | $\frac{π}{3}-\frac{{\sqrt{3}}}{2}$ | B. | $\frac{π}{3}-\frac{{\sqrt{3}}}{4}$ | C. | $\frac{π}{6}-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{π}{6}-\frac{{\sqrt{3}}}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
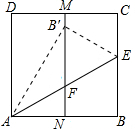 如图,正方形ABCD中,M,N分别是DC、AB的中点,沿过点A的直线折叠,使点B落在MN上,落点为B′,折痕交BC于点E,交MN于点F,再把这个正方形展开,若B′F=3cm,则AB=3$\sqrt{3}$cm.
如图,正方形ABCD中,M,N分别是DC、AB的中点,沿过点A的直线折叠,使点B落在MN上,落点为B′,折痕交BC于点E,交MN于点F,再把这个正方形展开,若B′F=3cm,则AB=3$\sqrt{3}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
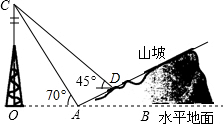 如图,小李在山坡坡脚A处测得他所在小区信号塔塔尖C的仰角为70°,在山坡上的点D处有一坐台,在点D处测得点C的仰角为45°,经侧量知信号塔塔底O距离山坡坡脚A的距离为200米,坡面的铅直高度与水平宽度的比为1:2,试根据以上数据求出信号塔塔尖:C与坐台D的距离.(结果保留整数,参考数据:cos70°≈0.34,sin70°≈0.94,tan70°≈2.75,$\sqrt{2}$=1.41)
如图,小李在山坡坡脚A处测得他所在小区信号塔塔尖C的仰角为70°,在山坡上的点D处有一坐台,在点D处测得点C的仰角为45°,经侧量知信号塔塔底O距离山坡坡脚A的距离为200米,坡面的铅直高度与水平宽度的比为1:2,试根据以上数据求出信号塔塔尖:C与坐台D的距离.(结果保留整数,参考数据:cos70°≈0.34,sin70°≈0.94,tan70°≈2.75,$\sqrt{2}$=1.41)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某公路隧道横截面为抛物线,其最大高度为6米,底部宽度AB长12米.
如图,某公路隧道横截面为抛物线,其最大高度为6米,底部宽度AB长12米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com