Question

18．在半径为5cm的圆内有长为5cm的弦AB，则此弦所对的圆周角为30°或150°．

Answer 1

分析 首先根据题意画出图形，然后在优弧AB上取点C，连接AC，BC，在劣弧上取点D，连接AD，BD，由⊙O的半径为5cm，弦AB的长为5cm，易得△OAB是等边三角形，继而求得答案．

解答 解：如图所示：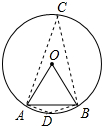
在优弧AB上取点C，连接AC，BC，在劣弧上取点D，连接AD，BD，
∵⊙O的半径为5cm，弦AB的长为5cm，
∴OA=OB=AB，
∴△OAB是等边三角形，
∴∠AOB=60°，
∴∠C=$\frac{1}{2}$∠AOB=30°，
∴∠D=180°-∠C=150°．
∴弦AB所对的圆周角的度数是：30°或150°．
故答案为：30°或150°．

点评 此题考查了圆周角定理以及等边三角形的判定与性质．注意根据题意画出图形，结合图形求解是关键．