Question

【题目】如图，∠AOP＝∠BOP＝15°，PC∥OA，PD⊥OA，若PC＝4，则PD的长为_____．

Answer 1

【答案】2

【解析】

过P作PE垂直与OB，由∠AOP＝∠BOP，PD垂直于OA，利用角平分线定理得到PE＝PD，由PC与OA平行，根据两直线平行得到一对内错角相等，又OP为角平分线得到一对角相等，等量代换可得∠COP＝∠CPO，又∠ECP为三角形COP的外角，利用三角形外角的性质求出∠ECP＝30°，在直角三角形ECP中，由30°角所对的直角边等于斜边的一半，由斜边PC的长求出PE的长，即为PD的长．

过P作PE⊥OB，交OB与点E，

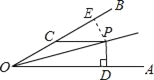
∵∠AOP＝∠BOP，PD⊥OA，PE⊥OB，

∴PD＝PE，

∵PC∥OA，

∴∠CPO＝∠POD，

又∠AOP＝∠BOP＝15°，

∴∠CPO＝∠BOP＝15°，

又∠ECP为△OCP的外角，

∴∠ECP＝∠COP+∠CPO＝30°，

在直角三角形CEP中，∠ECP＝30°，PC＝4，

∴PE＝PC＝2，

则PD＝PE＝2．

故答案为：2．