
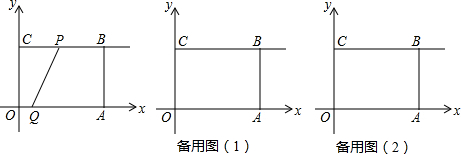
分析 (1)可求得P点坐标,由O、P、A的坐标,利用待定系数法可求得抛物线解析式;
(2)当t=2s时,可知P与点B重合,在Rt△ABQ中可求得tan∠QPA的值;
(3)用t可表示出BP和AQ的长,由△PBM∽△QAM可得到关于t的方程,可求得t的值;
(4)当点Q在线段OA上时,S=S△CPQ;当点Q在线段OA上,且点P在线段CB的延长线上时,由相似三角形的性质可用t表示出AM的长,由S=S四边形BCQM=S矩形OABC-S△COQ-S△AMQ,可求得S与t的关系式;当点Q在OA的延长线上时,设CQ交AB于点M,利用△AQM∽△BCM可用t表示出AM,从而可表示出BM,S=S△CBM,可求得答案.
解答 解:
(1)当t=1s时,则CP=2,
∵OC=3,四边形OABC是矩形,
∴P(2,3),且A(4,0),
∵抛物线过原点O,
∴可设抛物线解析式为y=ax2+bx,
∴$\left\{\begin{array}{l}{4a+2b=3}\\{16a+4b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-\frac{3}{4}}\\{b=3}\end{array}\right.$,
∴过O、P、A三点的抛物线的解析式为y=-$\frac{3}{4}$x2+3x;
(2)当t=2s时,则CP=2×2=4=BC,即点P与点B重合,OQ=2,如图1,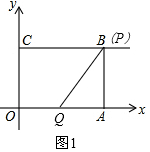
∴AQ=OA-OQ=4-2=2,且AP=OC=3,
∴tan∠QPA=$\frac{AQ}{AP}$=$\frac{2}{3}$;
(3)当线段PQ与线段AB相交于点M,则可知点Q在线段OA上,点P在线段CB的延长线上,如图2,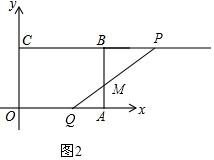
则CP=2t,OQ=t,
∴BP=PC-CB=2t-4,AQ=OA-OQ=4-t,
∵PC∥OA,
∴△PBM∽△QAM,
∴$\frac{BP}{AQ}$=$\frac{BM}{AM}$,且BM=2AM,
∴$\frac{2t-4}{4-t}$=2,解得t=3,
∴当线段PQ与线段AB相交于点M,且BM=2AM时,t为3s;
(4)当0≤t≤2时,如图3,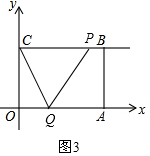
由题意可知CP=2t,
∴S=S△PCQ=$\frac{1}{2}$×2t×3=3t;
当2<t≤4时,设PQ交AB于点M,如图4,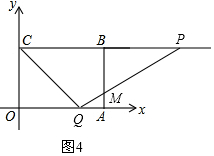
由题意可知PC=2t,OQ=t,则BP=2t-4,AQ=4-t,
同(3)可得$\frac{BP}{AQ}$=$\frac{BM}{AM}$=$\frac{2t-4}{4-t}$,
∴BM=$\frac{2t-4}{4-t}$•AM,
∴3-AM=$\frac{2t-4}{4-t}$•AM,解得AM=$\frac{12-3t}{t}$,
∴S=S四边形BCQM=S矩形OABC-S△COQ-S△AMQ=3×4-$\frac{1}{2}$×t×3-$\frac{1}{2}$×(4-t)×$\frac{12-3t}{t}$=24-$\frac{24}{t}$-3t;
当t>4时,设CQ与AB交于点M,如图5,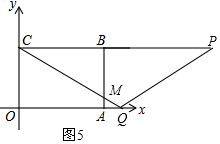
由题意可知OQ=t,AQ=t-4,
∵AB∥OC,
∴$\frac{AM}{OC}$=$\frac{AQ}{OQ}$,即$\frac{AM}{3}$=$\frac{t-4}{t}$,解得AM=$\frac{3t-12}{t}$,
∴BM=3-$\frac{3t-12}{t}$=$\frac{12}{t}$,
∴S=S△BCM=$\frac{1}{2}$×4×$\frac{12}{t}$=$\frac{24}{t}$;
综上可知S=$\left\{\begin{array}{l}{3t(0≤t≤2)}\\{24-\frac{24}{t}-3t(2<t≤4)}\\{\frac{24}{t}(t>4)}\end{array}\right.$.
点评 本题为二次函数与四边形的综合应用,涉及待定系数法、矩形的性质、相似三角形的判定和性质、三角函数的定义、方程思想及分类讨论思想等知识.在(1)中求得P点坐标是解题的关键,在(2)中确定P、B重合是解题的关键,在(3)中由相似三角形的性质得到关于t的方程是解题的关键,在(4)中确定出P、Q的位置,从而确定出S为哪一部分图形的面积是解题的关键.本题为“运动型”问题,用t和速度表示出相应线段的长度,化“动”为“静”是解这类问题的一般思路.本题考查知识点较多,综合性较强,特别是最后一问,情况较多,难度较大.


科目:初中数学 来源: 题型:选择题
| A. | 3a-2a=a | B. | $\sqrt{2}+\sqrt{5}$=$\sqrt{7}$ | C. | (2a)3=2a3 | D. | a6÷a3=a2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
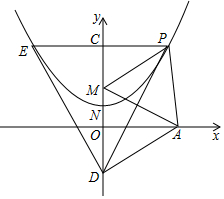 如图,已知抛物线的对称轴是y轴,且点(2,2),(1,$\frac{5}{4}$)在抛物线上,点P是抛物线上不与顶点N重合的一动点,过P作PA⊥x轴于A,PC⊥y轴于C,延长PC交抛物线于E,设M是O关于抛物线顶点N的对称点,D是C点关于N的对称点.
如图,已知抛物线的对称轴是y轴,且点(2,2),(1,$\frac{5}{4}$)在抛物线上,点P是抛物线上不与顶点N重合的一动点,过P作PA⊥x轴于A,PC⊥y轴于C,延长PC交抛物线于E,设M是O关于抛物线顶点N的对称点,D是C点关于N的对称点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 年龄(岁) | 12 | 13 | 14 | 15 |
| 人数(名) | 2 | 4 | 3 | 1 |
| A. | 12 | B. | 13 | C. | 13.5 | D. | 14 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.96×107km2 | B. | 960×104km2 | C. | 9.6×106km2 | D. | 9.6×105km2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在平行四边形ABCD中,点E是边AD上一点,且AE=2ED,EC交对角线BD于点F,则$\frac{{S}_{△EDF}}{{S}_{△CBF}}$等于( )
在平行四边形ABCD中,点E是边AD上一点,且AE=2ED,EC交对角线BD于点F,则$\frac{{S}_{△EDF}}{{S}_{△CBF}}$等于( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{9}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com