
如图,直线l1:y=x与反比例函数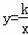
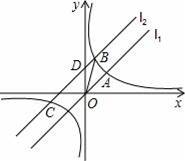
 的图象c相交于点A(2,a),将直线l1向上平移3个单位长度得到l2,直线l2与c相交于B,C两点,(点B在第一象限),交y轴于点D.
的图象c相交于点A(2,a),将直线l1向上平移3个单位长度得到l2,直线l2与c相交于B,C两点,(点B在第一象限),交y轴于点D.
(1)求反比例函数的表达式并写出图象为l2的一次函数的表达式;
(2)求B,C两点的坐标并求△BOD的面积.

【考点】反比例函数与一次函数的交点问题.
【专题】计算题.
【分析】(1)先把A(2,a)代入y=x可求出a确定A点坐标,再把A点坐标代入y=
 中可求出k的值,从而得到反比例函数解析式,然后利用一次函数的几何变换确定图象为l2的一次函数的表达式;
中可求出k的值,从而得到反比例函数解析式,然后利用一次函数的几何变换确定图象为l2的一次函数的表达式;
(2)通过解方程组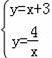
 可得B点和C点坐标,再求出直线y=x+3与y轴的交点D的坐标,然后根据三角形面积公式计算.
可得B点和C点坐标,再求出直线y=x+3与y轴的交点D的坐标,然后根据三角形面积公式计算.
【解答】解:(1)∵点A(2,a)在y=x上,
∴a=2,则A(2,2),
∵点A(2,2)在y=
 上,
上,
∴k=2×2=4,
∴反比例函数的解析式是y=
 ;
;
将y=x向上平移3个单位,得l2:y=x+3;
(2)解方程组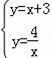
 得
得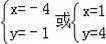
 ,
,
∴B(1,4),A(﹣4,﹣1),
当x=0时,y=x+3=3,则D(0,3),
∴S△OBD=
 ×3×1=
×3×1=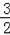
 .
.
【点评】本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.也考查了三角形面积公式.


科目:初中数学 来源: 题型:
已知反比例函数y=
 (k为常数,k≠1).
(k为常数,k≠1).
(Ⅰ)其图象与正比例函数y=x的图象的一个交点为P,若点P的纵坐标是2,求k的值;
(Ⅱ)若在其图象的每一支上,y随x的增大而减小,求k的取值范围;
(Ⅲ)若其图象的一支位于第二象限,在这一支上任取两点A(x1,y1)、B(x2,y2),当y1>y2时,试比较x1与x2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知双曲线y=
 (k>0)与直线y=
(k>0)与直线y=
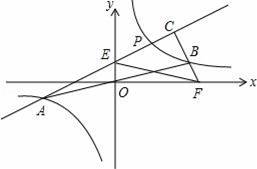
 x(k>0)交于A,B两点(点A在的B左侧)如图,点P是第一象限内双曲线上一动点,BC⊥AP于C,交x轴于F,PA交y轴于E,若AE2+BF2=m•EF2,则m= .
x(k>0)交于A,B两点(点A在的B左侧)如图,点P是第一象限内双曲线上一动点,BC⊥AP于C,交x轴于F,PA交y轴于E,若AE2+BF2=m•EF2,则m= .

查看答案和解析>>
科目:初中数学 来源: 题型:
九年级一班数学老师对全班学生在模拟考试中A卷成绩进行统计后,制成如下的统计表:
| 成绩(分) | 80 | 82 | 84 | 86 | 87 | 90 |
| 人数 | 8 | 12 | 9 | 3 | 5 | 8 |
则该班学生A卷成绩的众数和中位数分别是( )
A.82分,82分 B.82分,83分 C.80分,82分 D.82分,84分
查看答案和解析>>
科目:初中数学 来源: 题型:
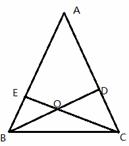
如图,三角形ABC内的线段BD、CE相交于点O,已知OB=OD,OC=2OE.若ΔBOC的面积=2,则四边形AEOD的面积等于……………………………………( )
A.4 B.5 C.6 D.7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com