
已知双曲线y=
 (k>0)与直线y=
(k>0)与直线y=
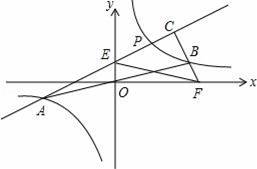
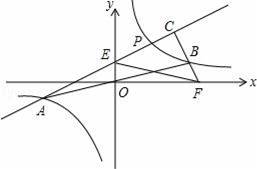
 x(k>0)交于A,B两点(点A在的B左侧)如图,点P是第一象限内双曲线上一动点,BC⊥AP于C,交x轴于F,PA交y轴于E,若AE2+BF2=m•EF2,则m= .
x(k>0)交于A,B两点(点A在的B左侧)如图,点P是第一象限内双曲线上一动点,BC⊥AP于C,交x轴于F,PA交y轴于E,若AE2+BF2=m•EF2,则m= .

1 .

【考点】反比例函数与一次函数的交点问题.
【分析】先求出A、B两点坐标,设点P(a,
 ),求出直线AP、BC得E、F两点坐标,利用两点间距离公式列出方程即可解决.
),求出直线AP、BC得E、F两点坐标,利用两点间距离公式列出方程即可解决.
【解答】解:由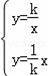
 解得
解得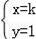
 ,或
,或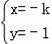
 ,
,
∴点A(﹣k,﹣1),B(k,1),
设点P(a,
 ),则直线AP为y=
),则直线AP为y=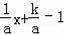
 ,直线BC为y=﹣ax+ak+1,
,直线BC为y=﹣ax+ak+1,
∴点E坐标(0,
 ﹣1),F坐标(k+
﹣1),F坐标(k+
 ,0),
,0),
∵AE2+BF2=m•EF2,
∴k2+(
 )2+
)2+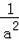
 +1=m[(k+
+1=m[(k+
 )2+(
)2+(
 ﹣1)2]
﹣1)2]
∴m(k2+(
 )2+
)2+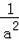
 +1)=k2+(
+1)=k2+(
 )2+
)2+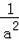
 +1,
+1,
∴m=1.
故答案为1.
【点评】本题考查一次函数、反比例函数以及勾股定理等有关知识,学会利用方程组求交点坐标,解题的关键是设参数a,想办法表示点E、F的坐标,题目有难度,有两个参数a、k,属于中考填空题中的压轴题.


科目:初中数学 来源: 题型:
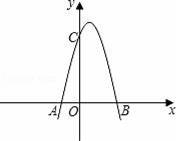
如图,已知抛物线与x轴交于点A(﹣2,0),B(4,0),与y轴交于点C(0,8).
(1)求抛物线的解析式及其顶点D的坐标;
(2)设直线CD交x轴于点E.在线段OB的垂直平分线上是否存在点P,使得点P到直线CD的距离等于点P到原点O的距离?如果存在,求出点P的坐标;如果不存在,请说明理由;
(3)过点B作x轴的垂线,交直线CD于点F,将抛物线沿其对称轴平移,使抛物线与线段EF总有公共点.试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?

查看答案和解析>>
科目:初中数学 来源: 题型:
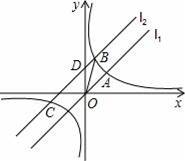
如图,直线l1:y=x与反比例函数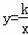
 的图象c相交于点A(2,a),将直线l1向上平移3个单位长度得到l2,直线l2与c相交于B,C两点,(点B在第一象限),交y轴于点D.
的图象c相交于点A(2,a),将直线l1向上平移3个单位长度得到l2,直线l2与c相交于B,C两点,(点B在第一象限),交y轴于点D.
(1)求反比例函数的表达式并写出图象为l2的一次函数的表达式;
(2)求B,C两点的坐标并求△BOD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
为绿化校园,某校计划购进A、B两种树苗,共21课.已知A种树苗每棵90元,B种树苗每棵70元.设购买B种树苗x棵,购买两种树苗所需费用为y元.
(1)y与x的函数关系式为: ;
(2)若购买B种树苗的数量少于A种树苗的数量,请给出一种费用最省的方案,并求出该方案所需费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com