
为绿化校园,某校计划购进A、B两种树苗,共21课.已知A种树苗每棵90元,B种树苗每棵70元.设购买B种树苗x棵,购买两种树苗所需费用为y元.
(1)y与x的函数关系式为: ;
(2)若购买B种树苗的数量少于A种树苗的数量,请给出一种费用最省的方案,并求出该方案所需费用.
【考点】一次函数的应用.
【分析】(1)根据购买两种树苗所需费用=A种树苗费用+B种树苗费用,即可解答;
(2)根据购买B种树苗的数量少于A种树苗的数量,列出不等式,确定x的取值范围,再根据(1)得出的y与x之间的函数关系式,利用一次函数的增减性结合自变量的取值即可得出更合算的方案.
【解答】解:(1)y=90(21﹣x)+70x=﹣20x+1890,
故答案为:y=﹣20x+1890.
(2)∵购买B种树苗的数量少于A种树苗的数量,
∴x<21﹣x,
解得:x<10.5,
又∵x≥1,
∴x的取值范围为:1≤x≤10,且x为整数,
∵y=﹣20x+1890,k=﹣20<0,
∴y随x的增大而减小,
∴当x=10时,y有最小值,最小值为:﹣20×10+1890=1690,
∴使费用最省的方案是购买B种树苗10棵,A种树苗11棵,所需费用为1690元.
【点评】题考查的是一元一次不等式及一次函数的应用,解决问题的关键是读懂题意,找到关键描述语,进而找到所求的量的等量关系和不等关系.


科目:初中数学 来源: 题型:
已知双曲线y=
 (k>0)与直线y=
(k>0)与直线y=
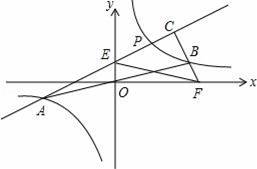
 x(k>0)交于A,B两点(点A在的B左侧)如图,点P是第一象限内双曲线上一动点,BC⊥AP于C,交x轴于F,PA交y轴于E,若AE2+BF2=m•EF2,则m= .
x(k>0)交于A,B两点(点A在的B左侧)如图,点P是第一象限内双曲线上一动点,BC⊥AP于C,交x轴于F,PA交y轴于E,若AE2+BF2=m•EF2,则m= .

查看答案和解析>>
科目:初中数学 来源: 题型:
九年级一班数学老师对全班学生在模拟考试中A卷成绩进行统计后,制成如下的统计表:
| 成绩(分) | 80 | 82 | 84 | 86 | 87 | 90 |
| 人数 | 8 | 12 | 9 | 3 | 5 | 8 |
则该班学生A卷成绩的众数和中位数分别是( )
A.82分,82分 B.82分,83分 C.80分,82分 D.82分,84分
查看答案和解析>>
科目:初中数学 来源: 题型:
对于二次函数y=﹣x2+2x.有下列四个结论:①它的对称轴是直线x=1;②设y1=﹣x12+2x1,y2=﹣x22+2x2,则当x2>x1时,有y2>y1;③它的图象与x轴的两个交点是(0,0)和(2,0);④当0<x<2时,y>0.其中正确的结论的个数为( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
把抛物线y=x2+1向左平移3个单位,再向下平移2个单位,得到的抛物线表达式为( )
A.y=(x﹣3)2+2 B.y=(x﹣3)2﹣1 C.y=(x+3)2﹣1 D.y=(x﹣3)2﹣2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com