
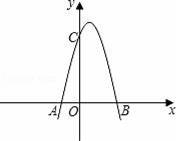
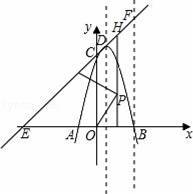
如图,已知抛物线与x轴交于点A(﹣2,0),B(4,0),与y轴交于点C(0,8).
(1)求抛物线的解析式及其顶点D的坐标;
(2)设直线CD交x轴于点E.在线段OB的垂直平分线上是否存在点P,使得点P到直线CD的距离等于点P到原点O的距离?如果存在,求出点P的坐标;如果不存在,请说明理由;
(3)过点B作x轴的垂线,交直线CD于点F,将抛物线沿其对称轴平移,使抛物线与线段EF总有公共点.试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?

【考点】二次函数综合题.
【专题】压轴题.
【分析】(1)由抛物线过A、B、C三点可求出抛物线表达式;
(2)假设存在,设出P点,解出直线CD的解析式,根据点P到CD的距离等于PO可解出P点坐标;
(3)应分两种情况:抛物线向上或下平移,设出解析式,代入点求出平移的单位长度.
【解答】解:(1)设抛物线解析式为y=a(x+2)(x﹣4).
把C(0,8)代入,得a=﹣1.
∴y=﹣x2+2x+8=﹣(x﹣1)2+9,
顶点D(1,9);
(2)假设满足条件的点P存在.依题意设P(2,t).
由C(0,8),D(1,9)求得直线CD的解析式为y=x+8,
它与x轴的夹角为45°.
设OB的中垂线交CD于H,则H(2,10).
则PH=|10﹣t|,点P到CD的距离为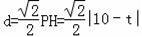
 .
.
又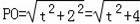
 .
.
∴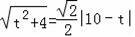
 .
.
平方并整理得:t2+20t﹣92=0,解之得t=﹣10±8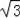
 .
.
∴存在满足条件的点P,P的坐标为(2,﹣10±8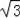
 ).
).
(3)由上求得E(﹣8,0),F(4,12).
①若抛物线向上平移,可设解析式为y=﹣x2+2x+8+m(m>0).
当x=﹣8时,y=﹣72+m.
当x=4时,y=m.
∴﹣72+m≤0或m≤12.
∴0<m≤72.
②若抛物线向下平移,可设解析式为y=﹣x2+2x+8﹣m(m>0).
由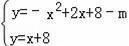
 ,
,
有﹣x2+x﹣m=0.
∴△=1﹣4m≥0,
∴m≤
 .
.
∴向上最多可平移72个单位长,向下最多可平移
 个单位长.
个单位长.

【点评】此题考查待定系数求抛物线解析式,第二问考查垂直平分线性质,利用距离相等解题,最后一问考抛物线的平移,要注意已知条件和技巧.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
下列因式分解正确的是( )
A.m2+n2=(m+n)(m﹣n) B.x2+2x﹣1=(x﹣1)2
C.a2﹣a=a(a﹣1) D.a2+2a+1=a(a+2)+1
查看答案和解析>>
科目:初中数学 来源: 题型:
已知反比例函数y=
 (k为常数,k≠1).
(k为常数,k≠1).
(Ⅰ)其图象与正比例函数y=x的图象的一个交点为P,若点P的纵坐标是2,求k的值;
(Ⅱ)若在其图象的每一支上,y随x的增大而减小,求k的取值范围;
(Ⅲ)若其图象的一支位于第二象限,在这一支上任取两点A(x1,y1)、B(x2,y2),当y1>y2时,试比较x1与x2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知双曲线y=
 (k>0)与直线y=
(k>0)与直线y=
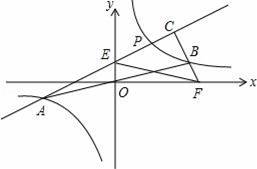
 x(k>0)交于A,B两点(点A在的B左侧)如图,点P是第一象限内双曲线上一动点,BC⊥AP于C,交x轴于F,PA交y轴于E,若AE2+BF2=m•EF2,则m= .
x(k>0)交于A,B两点(点A在的B左侧)如图,点P是第一象限内双曲线上一动点,BC⊥AP于C,交x轴于F,PA交y轴于E,若AE2+BF2=m•EF2,则m= .

查看答案和解析>>
科目:初中数学 来源: 题型:
对于二次函数y=﹣x2+2x.有下列四个结论:①它的对称轴是直线x=1;②设y1=﹣x12+2x1,y2=﹣x22+2x2,则当x2>x1时,有y2>y1;③它的图象与x轴的两个交点是(0,0)和(2,0);④当0<x<2时,y>0.其中正确的结论的个数为( )
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com