练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    化简求值：（3a+b）2﹣（3a﹣b）（3a+b）﹣5b（a﹣b），其中a=1，b=﹣2．


    【考点】整式的混合运算—化简求值．

    【分析】原式利用完全平方公式，平方差公式，以及单项式乘以多项式法则计算，去括号合并得到最简结果，把a与b的值代入计算即可求出值．

    【解答】解：原式=9a2+6ab+b2﹣9a2+b2﹣5ab+5b2=ab+7b2，

    当a=1，b=﹣2，原式=﹣2+28=26．

    　


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    在一个口袋中有4个完全相同的小球，它们的标号分别为1，2，3，4，一人从中随机摸出一球记下标号后放回，再从中随机摸出一个小球记下标号，则两次摸出的小球的标号之和大于4的概率是　　　　　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    ．如图．直线y=ax+b与双曲线相交于两点A（1，2），B（m，﹣4）．

    （1）求直线与双曲线的解析式；

    （2）求不等式ax+b＞的解集（直接写出答案）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，将四个“米”字格的正方形内涂上阴影，其中既是轴对称图形，又是中心对称图形的是（　　）

    A．     B．     C．     D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


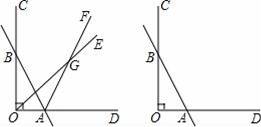
    已知如图，∠COD=90°，直线AB与OC交于点B，与OD交于点A，射线OE和射线AF交于点G．

    （1）若OE平分∠BOA，AF平分∠BAD，∠OBA=30°，则∠OGA=　　　　　　

    （2）若∠GOA=∠BOA，∠GAD=∠BAD，∠OBA=30°，则∠OGA=　　　　　　

    （3）将（2）中“∠OBA=30°”改为“∠OBA=α”，其余条件不变，则∠OGA=　　　　　　（用含α的代数式表示）

    （4）若OE将∠BOA分成1：2两部分，AF平分∠BAD，∠ABO=α（30°＜α＜90°），求∠OGA的度数（用含α的代数式表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    （x﹣y）2﹣（x﹣2y）（x+2y）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在（x+1）（2x2+ax+1）的运算结果中x2的系数是﹣1，那么a的值是　　　　　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


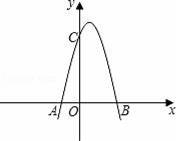
    如图，已知抛物线与x轴交于点A（﹣2，0），B（4，0），与y轴交于点C（0，8）．

    （1）求抛物线的解析式及其顶点D的坐标；

    （2）设直线CD交x轴于点E．在线段OB的垂直平分线上是否存在点P，使得点P到直线CD的距离等于点P到原点O的距离？如果存在，求出点P的坐标；如果不存在，请说明理由；

    （3）过点B作x轴的垂线，交直线CD于点F，将抛物线沿其对称轴平移，使抛物线与线段EF总有公共点．试探究：抛物线向上最多可平移多少个单位长度？向下最多可平移多少个单位长度？

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若关于x的一元二次方程x2﹣2x+m=0有实数根，则m的取值范围是　　　　　　．

    查看答案和解析>>

    同步练习册答案