
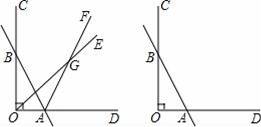
已知如图,∠COD=90°,直线AB与OC交于点B,与OD交于点A,射线OE和射线AF交于点G.
(1)若OE平分∠BOA,AF平分∠BAD,∠OBA=30°,则∠OGA=
(2)若∠GOA=
 ∠BOA,∠GAD=
∠BOA,∠GAD=
 ∠BAD,∠OBA=30°,则∠OGA=
∠BAD,∠OBA=30°,则∠OGA=
(3)将(2)中“∠OBA=30°”改为“∠OBA=α”,其余条件不变,则∠OGA= (用含α的代数式表示)
(4)若OE将∠BOA分成1:2两部分,AF平分∠BAD,∠ABO=α(30°<α<90°),求∠OGA的度数(用含α的代数式表示)

【考点】三角形内角和定理;三角形的外角性质.
【分析】(1)由于∠BAD=∠ABO+∠BOA=α+90°,由AF平分∠BAD得到∠FAD=
 ∠BAD,而∠FAD=∠EOD+∠OGA,2×45°+2∠OGA=α+90°,则∠OGA=
∠BAD,而∠FAD=∠EOD+∠OGA,2×45°+2∠OGA=α+90°,则∠OGA=
 α,然后把α=30°代入计算即可;
α,然后把α=30°代入计算即可;
(2)由于∠GOA=
 ∠BOA=30°,∠GAD=
∠BOA=30°,∠GAD=
 ∠BAD,∠OBA=α,根据∠FAD=∠EOD+∠OGA得到3×30°+3∠OGA=α+90°,则∠OGA=
∠BAD,∠OBA=α,根据∠FAD=∠EOD+∠OGA得到3×30°+3∠OGA=α+90°,则∠OGA=
 α,然后把α=30°代入计算;
α,然后把α=30°代入计算;
(3)由(2)得到∠OGA=
 α;
α;
(4)讨论:当∠EOD:∠COE=1:2时,利用∠BAD=∠ABO+∠BOA=α+90°,∠FAD=∠EOD+∠OGA得到2×30°+2∠OGA=α+90°,则∠OGA=
 α+15°;
α+15°;
当∠EOD:∠COE=2:1时,则∠EOD=60°,同理得∠OGA=
 α﹣15°.
α﹣15°.
【解答】解:(1)15°;
(2)10°;
(3)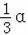
 ;
;
(4)当∠EOD:∠COE=1:2时,
则∠EOD=30°,
∵∠BAD=∠ABO+∠BOA=α+90°,
而AF平分∠BAD,
∴∠FAD=
 ∠BAD,
∠BAD,
∵∠FAD=∠EOD+∠OGA,
∴2×30°+2∠OGA=α+90°,
∴∠OGA=
 α+15°;
α+15°;
当∠EOD:∠COE=2:1时,则∠EOD=60°,
同理得到∠OGA=
 α﹣15°,
α﹣15°,
即∠OGA的度数为
 α+15°或
α+15°或
 α﹣15°.
α﹣15°.
故答案为15°,10°,
 α.
α.




 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
遵义市某中学为了搞好“创建全国文明城市”的宣传活动,对本校部分学生(随机抽查)进行了一次相关知识了解程度的调查测试(成绩分为A、B、C、D、E五个组,x表示测试成绩).通过对测试成绩的分析,得到如图所示的两幅不完整的统计图.请你根据图中提供的信息解答以下问题:


(1)参加调查测试的学生为 人;
(2)将条形统计图补充完整;
(3)本次调查测试成绩中的中位数落在 组内;
(4)若测试成绩在80分以上(含80分)为优秀,该中学共有学生2600人,请你根据样本数据估计全校学生测试成绩为优秀的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
在平面直角坐标系中,正方形A1B1C1D1、D1E1E2B2、A2B2C2D2、D2E3E4B3、A3B3C3D3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…则正方形A2015B2015C2015D2015的边长是( )


A.(
 )2014 B.(
)2014 B.(
 )2015 C.(
)2015 C.(
 )2015 D.(
)2015 D.(
 )2014
)2014
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com