
��ƽ��ֱ������ϵ�У�������A1B1C1D1��D1E1E2B2��A2B2C2D2��D2E3E4B3��A3B3C3D3������ͼ��ʾ�ķ�ʽ���ã����е�B1��y���ϣ���C1��E1��E2��C2��E3��E4��C3����x���ϣ���֪������A1B1C1D1�ı߳�Ϊ1����B1C1O=60�㣬B1C1��B2C2��B3C3����������A2015B2015C2015D2015�ı߳��ǣ�������


A����
 ��2014 B����
��2014 B����
 ��2015 C����
��2015 C����
 ��2015 D����
��2015 D����
 ��2014
��2014
��
D�����㡿�����ε����ʣ�
��ר�⡿ѹ���⣻�����ͣ�
�����������������ε����ʽ��������Ǻ�����ϵ�ó������εı߳��������ó��仯���ɼ��ɵó��𰸣�
����𡿷���һ��
�⣺��ͼ��ʾ����������A1B1C1D1�ı߳�Ϊ1����B1C1O=60�㣬B1C1��B2C2��B3C3��
��D1E1=B2E2��D2E3=B3E4����D1C1E1=��C2B2E2=��C3B3E4=30�㣬
��D1E1=C1D1sin30��=
 ����B2C2=��
����B2C2=��
 ��1��
��1��
ͬ���ɵã�B3C3=
 =��
=��
 ��2��
��2��
��������AnBnCnDn�ı߳��ǣ���
 ��n��1��
��n��1��
��������A2015B2015C2015D2015�ı߳��ǣ���
 ��2014��
��2014��
��ѡ��D��
��������
��������A1B1C1D1�ı߳�Ϊ1��
��B1C1O=60�㣬
��D1E1=B2E2=
 ��
��
��B1C1��B2C2��B3C3��
���E2B2C2=60�㣬
��B2C2=
 ��
��
ͬ����
B3C3=
 ��
��
 =
=
 ��
��
��a1=1��q=
 ��
��
��������A2015B2015C2015D2015�ı߳�=1��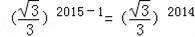
 ��
��
��������������Ҫ�����������ε������Լ�������Ǻ�����ϵ���ó������εı߳��仯�����ǽ���ؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
��֪��ABC�������������е�λ����ͼ��ʾ����A��B��C��P���ڸ���ϣ����P������ABC�ģ�������
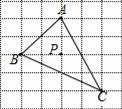

A������ B������ C������ D����ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����ͼ��ֱ��y=ax+b��˫����
 �ཻ������A��1��2����B��m����4����
�ཻ������A��1��2����B��m����4����
��1����ֱ����˫���ߵĽ���ʽ��
��2����ʽax+b��
 �Ľ⼯��ֱ��д���𰸣�
�Ľ⼯��ֱ��д���𰸣�


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ��CD�ǡ�O��ֱ����A��B�ǡ�O�ϵ����㣬����B=20�㣬���ADC�Ķ���Ϊ��������������


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ�����ĸ����ס��ָ����������Ϳ����Ӱ�����м�����Գ�ͼ�Σ��������ĶԳ�ͼ�ε��ǣ�������
A��
 B��
B��
 C��
C��
 D��
D��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
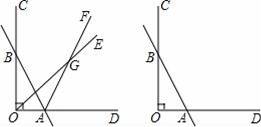
��֪��ͼ����COD=90�㣬ֱ��AB��OC���ڵ�B����OD���ڵ�A������OE������AF���ڵ�G��
��1����OEƽ�֡�BOA��AFƽ�֡�BAD����OBA=30�㣬���OGA=������������
��2������GOA=
 ��BOA����GAD=
��BOA����GAD=
 ��BAD����OBA=30�㣬���OGA=������������
��BAD����OBA=30�㣬���OGA=������������
��3������2���С���OBA=30�㡱��Ϊ����OBA=�����������������䣬���OGA=���������������ú����Ĵ���ʽ��ʾ��
��4����OE����BOA�ֳ�1��2�����֣�AFƽ�֡�BAD����ABO=����30�㣼����90�㣩�����OGA�Ķ������ú����Ĵ���ʽ��ʾ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�ڣ�x+1����2x2+ax+1������������x2��ϵ���ǩ�1����ôa��ֵ����������������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com