
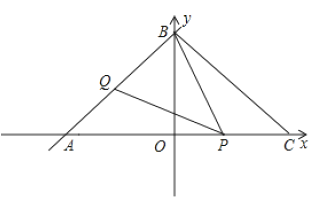
【题目】如图,一次函数![]() 的图象与
的图象与![]() ,
,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,点
两点,点![]() 与点
与点![]() 关于
关于![]() 轴对称.动点
轴对称.动点![]() ,
,![]() 分别在线段
分别在线段![]() ,
,![]() 上(点
上(点![]() 与点
与点![]() ,
,![]() 不重合),且满足
不重合),且满足![]() .
.
(1)求点![]() ,
,![]() 的坐标及线段
的坐标及线段![]() 的长度;
的长度;
(2)当点![]() 在什么位置时,
在什么位置时,![]() ,说明理由;
,说明理由;
(3)当![]() 为等腰三角形时,求点
为等腰三角形时,求点![]() 的坐标.
的坐标.
【答案】(1)10;(2)当点![]() 的坐标是
的坐标是![]() 时,
时,![]() ;(3)点
;(3)点![]() 的坐标是
的坐标是![]() 或
或![]() .
.
【解析】
(1)利用一次函数图象上点的坐标特征可求出点![]() ,
,![]() 的坐标,结合点
的坐标,结合点![]() 与点
与点![]() 关于
关于![]() 轴对称可得出点
轴对称可得出点![]() 的坐标,进而可得出线段
的坐标,进而可得出线段![]() 的长度;
的长度;
(2)当点![]() 的坐标是
的坐标是![]() 时,
时,![]() ,由点
,由点![]() ,
,![]() 的坐标可得出
的坐标可得出![]() 的长度,由勾股定理可求出
的长度,由勾股定理可求出![]() 的长度,进而可得出
的长度,进而可得出![]() ,通过角的计算及对称的性质可得出
,通过角的计算及对称的性质可得出![]() ,
,![]() ,结合
,结合![]() 可证出
可证出![]() ,由此可得出:当点
,由此可得出:当点![]() 的坐标是
的坐标是![]() 时,
时,![]() ;
;
(3)分![]() ,
,![]() 及
及![]() 三种情况考虑:①当
三种情况考虑:①当![]() 时,由(2)的结论结合全等三角形的性质可得出当点
时,由(2)的结论结合全等三角形的性质可得出当点![]() 的坐标是
的坐标是![]() 时
时![]() ;②当
;②当![]() 时,利用等腰三角形的性质结合
时,利用等腰三角形的性质结合![]() 可得出
可得出![]() ,利用三角形外角的性质可得出
,利用三角形外角的性质可得出![]() ,进而可得出此种情况不存在;③当
,进而可得出此种情况不存在;③当![]() 时,利用等腰三角形的性质结合
时,利用等腰三角形的性质结合![]() 可得出
可得出![]() ,设此时
,设此时![]() 的坐标是
的坐标是![]() ,在
,在![]() 中利用勾股定理可得出关于
中利用勾股定理可得出关于![]() 的一元一次方程,解之即可得出结论.综上,此题得解.
的一元一次方程,解之即可得出结论.综上,此题得解.
解:(1)当![]() 时,
时,![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ;
;
当![]() 时,
时,![]() ,解得:
,解得:![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ;
;
![]() 点
点![]() 与点
与点![]() 关于
关于![]() 轴对称,
轴对称,
![]() 点
点![]() 的坐标为
的坐标为![]() ,
,
![]() .
.
(2)当点![]() 的坐标是
的坐标是![]() 时,
时,![]() ,理由如下:
,理由如下:
![]() 点
点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,
![]()
![]() ,
,
![]() .
.
![]() ,
,![]() ,
,![]() ,
,
![]() .
.
![]() 和
和![]() 关于
关于![]() 轴对称,
轴对称,
![]() .
.
在![]() 和
和![]() 中
中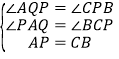 ,
,
![]() .
.
![]() 当点
当点![]() 的坐标是
的坐标是![]() 时,
时,![]() .
.
(3)分为三种情况:
①当![]() 时,如图1所示,由(2)知,当点
时,如图1所示,由(2)知,当点![]() 的坐标是
的坐标是![]() 时,
时,
![]()
![]() ,
,
![]() 此时
此时![]() 点的坐标是
点的坐标是![]() ;
;
②当![]() 时,则
时,则![]() ,
,
![]() ,
,
![]() .
.
而根据三角形的外角性质得:![]() ,
,
![]() 此种情况不存在;
此种情况不存在;
③当![]() 时,则
时,则![]() ,
,
![]() ,如图2所示.
,如图2所示.
设此时![]() 的坐标是
的坐标是![]() ,
,
在![]() 中,由勾股定理得:
中,由勾股定理得:
![]() ,
,
![]() ,
,
解得:![]() ,
,
![]() 此时
此时![]() 的坐标是
的坐标是![]() .
.
综上所述:当![]() 为等腰三角形时,点
为等腰三角形时,点![]() 的坐标是
的坐标是![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】王老师给学生出了一道题:
求(2a+b)(2a﹣b)+2(2a﹣b)2+(2ab2﹣16a2b)÷(﹣2a)的值,其中a=![]() ,b=﹣1,同学们看了题目后发表不同的看法.小张说:条件b=﹣1是多余的.”小李说:“不给这个条件,就不能求出结果,所以不多余.”
,b=﹣1,同学们看了题目后发表不同的看法.小张说:条件b=﹣1是多余的.”小李说:“不给这个条件,就不能求出结果,所以不多余.”
(1)你认为他们谁说的有道理?为什么?
(2)若xm等于本題计算的结果,试求x2m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠BAC=90°,D是AC的中点,CE⊥BD于点E,交BA的延长线于点F.若BF=12,则△FBC的面积为( )

A. 40 B. 46 C. 48 D. 50
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:
(1)如图①,在等腰直角三角形ABC中,∠ACB=90,作CM平分∠ACB交AB于点M,点D为射线CM上一点,以点C为旋转中心将线段CD逆时针旋转90°得到线段CE,连接DE交射线CB于点F,连接BD、BE
填空:
①线段BD、BE的数量关系为______.
②线段BC、DE的位置关系为______.
推广:
(2)如图②,在等腰三角形ABC中,顶角∠ACB=a,作CM平分∠ACB交AB于点M,点D为△ABC外部射线CM上一点,以点C为旋转中心将线段CD逆时针旋转α度得到线段CE,连接DE、BD、BE请判断(1)中的结论是否成立,并说明理由.
应用:
(3)如图③,在等边三角形ABC中,AB=4.作BM平分∠ABC交AC于点M,点D为射线BM上一点,以点B为旋转中心将线段BD逆时针旋转60°得到线段BE,连接DE交射线BA于点F,连接AD、AE.当以A、D、M为顶点的三角形与△AEF全等时,请直接写出DE的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农场去年大豆和小麦的总产量为200吨,今年大豆和小麦的总产量为225吨,其中大豆比去年増产5%,小麦比去年増产15%,求该农场今年大豆和小麦的产量各是多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.

(1)求证:△CBG≌△CDG;
(2)求∠HCG的度数;并判断线段HG、OH、BG之间的数量关系,说明理由;
(3)连结BD、DA、AE、EB得到四边形AEBD,在旋转过程中,四边形AEBD能否为矩形?如果能,请求出点H的坐标;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2011次运动后,动点P的坐标是____________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(14分)小明到某服装商场进行社会调查,了解到该商场为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法,并获得如下信息:
营业员A:月销售件数200件,月总收入2400元;
营业员B:月销售件数300件,月总收入2700元;
假设营业员的月基本工资为![]() 元,销售每件服装奖励
元,销售每件服装奖励![]() 元.
元.
(1)求![]() 、
、![]() 的值;
的值;
(2)若某营业员的月总收入不低于3100元,那么他当月至少要卖服装多少件?
(3)商场为了多销售服装,对顾客推荐一种购买方式:如果购买甲3件,乙2件,丙1件共需350元;如果购买甲1件,乙2件,丙3件共需370元.某顾客想购买甲、乙、丙各一件共需多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
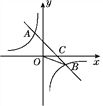
【题目】如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=![]() (k≠0)的图象交于第二、四象限的A,B两点,与x轴交于C点.已知A(-2,m),B(n,-2),tan ∠BOC=
(k≠0)的图象交于第二、四象限的A,B两点,与x轴交于C点.已知A(-2,m),B(n,-2),tan ∠BOC=![]() ,则此一次函数的解析式为________________.
,则此一次函数的解析式为________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com