
����Ŀ����ͼ��������ABCO�ı�OA��OC���������ϣ���B����Ϊ��6��6������������ABCO�Ƶ�C��ʱ����ת�ǶȦ���0�㣼����90�㣩���õ�������CDEF��ED���߶�AB�ڵ�G��ED���ӳ��߽��߶�OA�ڵ�H����CH��CG��

��1����֤����CBG�ա�CDG��
��2������HCG�Ķ��������ж��߶�HG��OH��BG֮���������ϵ��˵�����ɣ�
��3������BD��DA��AE��EB�õ��ı���AEBD������ת�����У��ı���AEBD�ܷ�Ϊ���Σ�����ܣ��������H�����ꣻ������ܣ���˵�����ɣ�
���𰸡���1��֤������������2��45����HG= HO+BG����3����2��0����
��������
�����������1����֤ȫ�ȣ��۲����������Σ����ֶ���ֱ�ǣ���CGΪ�����ߣ�����������һ��ֱ�DZ���ȼ��ɣ���Ϊ��Ϊ��������ת�õ������Ա߶���ȣ������ۿ�֤��
��2�����ʵĽ��ۣ�����һ�㶼Ҫʹ�ò�����������������������ȫ�ȿ��Եõ���Ӧ�ߡ�����ȣ���BG=DG����DCG=��BCG��ͬ��һ�ʵ�˼·��Ҳ��������CDH�ա�COH��Ҳ�ж�Ӧ�ߡ�����ȣ���OH=DH����OCH=��DCH��������GCHΪ![]() �Ľǵĺͣ��Ľ�ǡ�����ֱ�ǣ�������GCH=90���������õ�OH+BG=HG��
�Ľǵĺͣ��Ľ�ǡ�����ֱ�ǣ�������GCH=90���������õ�OH+BG=HG��
��3���ı���AEBD��Ϊ���Σ�������Ϊƽ���ı��Σ���Ҫ�Խ�����ƽ�֣����ʵĵ�ֻ��GΪAB�е��ʱ�����ϼ���֪DG=BG�����Դ�ʱͬʱ����DG=AG=EG=BG�����ı���AEBDΪ���Σ���H������꣬��������Ϊ��x��0������OH=x��AH=6-x����BGΪAB��һ�룬����DG=BG=AG=3�����ɣ�2����HG=x+3������Rt��HGA�У����߶������ú�x�ı���ʽ�����ô���ݹ��ɶ������з��̣��������x���Ƶ�H���꣮
�����������1����������ABCO�Ƶ�C��ת�õ�������CDEF
��CD=CB����CDG=��CBG=90��
��Rt��CDG��Rt��CBG��
![]()
���CDG�ա�CBG��HL����
��2���ߡ�CDG�ա�CBG
���DCG=��BCG��DG=BG
��Rt��CHO��Rt��CHD��
![]()
���CHO�ա�CHD��HL��
���OCH=��DCH��OH=DH
��![]()
HG=HD+DG=HO+BG
��3���ı���AEBD��Ϊ����
��ͼ��

����BD��DA��AE��EB
��Ϊ�ı���AEBD��Ϊ���Σ�������Ϊƽ���ı��Σ���Ҫ�Խ�����ƽ�֣����ʵĵ�ֻ��GΪAB�е��ʱ��
��ΪDG=BG�����Դ�ʱͬʱ����DG=AG=EG=BG����ƽ���ı���AEBD�Խ�����ȣ�����Ϊ���Σ�
���Ե�G��ΪAB�е�ʱ���ı���AEBDΪ���Σ�
���ı���DAEBΪ����
��AG=EG=BG=DG
��AB=6
��AG=BG=3
��H���������x��0��
��HO=x
��OH=DH��BG=DG
��HD=x��DG=3
��Rt��HGA��
��HG=x+3��GA=3��HA=6-x
�ࣨx+3��2=32+��6-x��2
��x=2
��H���������2��0����


 ���ɶ���ܲ��¿�ֱͨ�п�ϵ�д�
���ɶ���ܲ��¿�ֱͨ�п�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2015��6��27�գ��Ĵ�����ͼ�����ί���������Ļ��ݾٰ��˵ڶ��������ֽ��ѵ���μ���ѵ��С�����һ��Rt��ABC��ֽƬ��ȥһ�����BDEFֽƬ����ͼ��ʾ������C=30�㣬AB=10cm����þ���BDEF��������Ϊ��������
A.4![]() cm3
cm3
B.5![]() cm3
cm3
C.10![]() cm3
cm3
D.25![]() cm3
cm3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
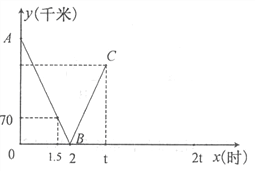
����Ŀ��һ���쳵�Ӽ�ʻ���ҵأ�һ���������ҵ�ʻ���أ�����ͬʱ������������ʻ.����ʻ��ʱ��Ϊx(ʱ)������֮��ľ���Ϊy(ǧ��)��ͼ�е����߱�ʾ�������������쳵�����ҵع�����y��x֮��ĺ�����ϵ������ͼ����Ϣ��
��1�����߶�AB����ֱ�ߵĺ�������ʽ��
��2�� ����ü�������֮��ľ���Ϊ ǧ�ף�
��3����֪��������ʱ�쳵����180ǧ�ף���쳵�Ӽص����ҵ�����ʱ��Ϊ Сʱ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
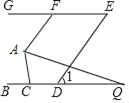
����Ŀ����ͼ����֪BC��GE��AF��DE����1=56�㣮
��1������AFG�Ķ�����
��2����AQƽ����FAC����BC�ڵ�Q������Q=14�㣬����ACB�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬��A������Ϊ��1��a������B������Ϊ��b��1������C������Ϊ��c��0��������a��b���㣨a+b��8��2+|a��b+2|=0��
��1����A��B��������ꣻ
��2������ABC�����Ϊ6ʱ�����C�����ꣻ
��3����4��S��ABC��10ʱ�����C�ĺ�����c��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB=12��BC=15��AD��BC�ڵ�D����BAD=30�㣬��tanC��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��һ���ң���AB=4![]() �� ��C��E�ֱ��ڡ�O�ϣ���OC��AB�ڵ�D����E=30�㣬����OA��
�� ��C��E�ֱ��ڡ�O�ϣ���OC��AB�ڵ�D����E=30�㣬����OA��
��1����OA�ij���
��2����AF�ǡ�O����һ���ң��ҵ�O��AF�ľ���Ϊ2![]() �� ֱ��д����BAF�Ķ�����
�� ֱ��д����BAF�Ķ�����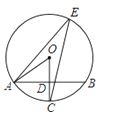
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ͼ������OEFPMN��������ij��������ʻ�������ٶ���ʱ��ĺ�����ϵ������˵���д�����ǣ� ��

A. ��3��ʱ�������ٶ���40ǧ��/ʱ
B. ��12��ʱ�������ٶ���0ǧ��/ʱ
C. �ӵ�3�ֵ���6�֣�������ʻ��120ǧ��
D. �ӵ�9�ֵ���12�֣��������ٶȴ�60ǧ��/ʱ���ٵ�0ǧ��/ʱ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���P��y�������ڵ�C����P�İ뾶��4��ֱ��y=x����P�صõ���AB�ij�Ϊ4![]() �� ���P�����꣮
�� ���P�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com