
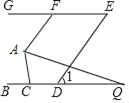
【题目】如图,已知BC∥GE,AF∥DE,∠1=56°.
(1)求∠AFG的度数;
(2)若AQ平分∠FAC,交BC于点Q,且∠Q=14°,求∠ACB的度数.
【答案】(1)56°,(2)84°.
【解析】
(1)先根据BC∥EG得出∠E=∠1=56°,再由AF∥DE可知∠AFG=∠E=56°;
(2)作AM∥BC,由平行线的传递性可知AM∥EG,故∠FAM=∠AFG,再根据AM∥BC可知∠QAM=∠Q,故∠FAQ=∠FAM+∠QAM,再根据AQ平分∠FAC可知∠MAC=∠QAC+∠QAM=84°,根据AM∥BC即可得出结论.
(1)∵BC∥EG,
∴∠E=∠1=56°.
∵AF∥DE,
∴∠AFG=∠E=56°;
(2)作AM∥BC,
∵BC∥EG,
∴AM∥EG,
∴∠FAM=∠AFG=56°.
∵AM∥BC,
∴∠QAM=∠Q=14°,
∴∠FAQ=∠FAM+∠QAM=70°.
∵AQ平分∠FAC,
∴∠QAC=∠FAQ=70°,
∴∠MAC=∠QAC+∠QAM=84°.
∵AM∥BC,
∴∠ACB=∠MAC=84°.


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠C=120°,AD=2AB=4,点H、G分别是边CD、BC上的动点.连接AH、HG,点E为AH的中点,点F为GH的中点,连接EF.则EF的最大值与最小值的差为( )

A. 1 B. ![]() ﹣1 C.
﹣1 C. ![]() D. 2﹣
D. 2﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
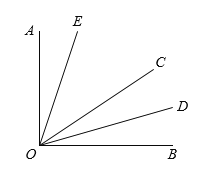
【题目】如图,∠AOC与∠BOC互余,OD平分∠BOC,∠EOC=2∠AOE.
(1)若∠AOD=75°,求∠AOE的度数.
(2)若∠DOE=54°,求∠EOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:AD平分∠CAE,AD∥BC.
(1)求证:△ABC是等腰三角形.
(2)当∠CAE等于多少度时△ABC是等边三角形?证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面推理过程
如图,已知DE∥BC,DF、BE分别平分∠ADE、∠ABC,可推得∠FDE=∠DEB的理由:

∵DE∥BC(已知)
∴∠ADE= .( )
∵DF、BE分别平分∠ADE、∠ABC,
∴∠ADF=![]() ,
,
∠ABE=![]() .( )
.( )
∴∠ADF=∠ABE
∴DF∥ .( )
∴∠FDE=∠DEB. ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,⊙C的半径为r,点P是与圆心C不重合的点,给出如下定义:若点P′为射线CP上一点,满足CPCP′=r2 , 则称点P′为点P关于⊙C的反演点.右图为点P及其关于⊙C的反演点P′的示意图.
(1)如图1,当⊙O的半径为1时,分别求出点M(1,0),N(0,2),T(![]() ,
, ![]() )关于⊙O的反演点M′,N′,T′的坐标;
)关于⊙O的反演点M′,N′,T′的坐标;
(2)如图2,已知点A(1,4),B(3,0),以AB为直径的⊙G与y轴交于点C,D(点C位于点D下方),E为CD的中点.
①若点O,E关于⊙G的反演点分别为O′,E′,求∠E′O′G的大小;
②若点P在⊙G上,且∠BAP=∠OBC,设直线AP与x轴的交点为Q,点Q关于⊙G的反演点为Q′,请直接写出线段GQ′的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.

(1)求证:△CBG≌△CDG;
(2)求∠HCG的度数;并判断线段HG、OH、BG之间的数量关系,说明理由;
(3)连结BD、DA、AE、EB得到四边形AEBD,在旋转过程中,四边形AEBD能否为矩形?如果能,请求出点H的坐标;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:AB=CD;
(2)若AB=CF,∠B=30°,求∠D的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,定义直线y=ax+b为抛物线y=ax2+bx的特征直线,C(a,b)为其特征点.设抛物线y=ax2+bx与其特征直线交于A、B两点(点A在点B的左侧).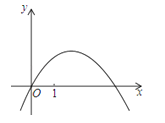
(1)当点A的坐标为(0,0),点B的坐标为(1,3)时,特征点C的坐标为 .
(2)若抛物线y=ax2+bx如图所示,请在所给图中标出点A、点B的位置;
(3)设抛物线y=ax2+bx的对称轴与x轴交于点D,其特征直线交y轴于点E,点F的坐标为(1,0),DE∥CF.
①若特征点C为直线y=﹣4x上一点,求点D及点C的坐标 ;
②若![]() <tan∠ODE<2,则b的取值范围是 .
<tan∠ODE<2,则b的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com